Ъгълът между правата линия и равнината

# 10070; Ъгълът между вектора и линията

# 10070; Ъгълът между правата линия и равнината

# 10070; Ъгълът между равнините

3. Проблеми с анализа

4. Задачи за независим решение

За да се реши проблема с намирането на ъгли, ще се въведе основните понятия.

Ако през точка в пространството проведе три взаимно перпендикулярни линии, всяка от които е избран, и посоката на избиране на устройството от сегменти, се казва, че Декартова координатна система в пространството.

Прав, с избрани области те са наречени координатни оси. но общата им точка - произход. Тя обикновено е обозначен с буквата О. Осите са определени, както следва: Ox, Oy, Оз - и има име: х-ос, у-ос Z-оста, съответно.

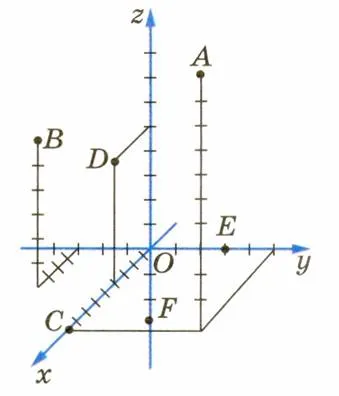
Фигурата показва шест точки с координати:

А (9, 5, 10) C (9; 0; 0) E (0, 3, 0)

В (4; -3 6) D (4, 0, 5) F (0, 0, -3)

А сега да разгледаме векторите. Всеки вектор може да се разлага в координатна вектор, т. Е. във формата. къде. вектори единица и разширяване коефициенти х, Y, Z са еднозначно определени.

х коефициентите, Y и Z вектори в разлагането на координатните вектори nazyvayutsyakoordinatami вектор в тази координатна система.

Като се има предвид вектор. Дължината на вектора (| |) е коренът на сумата от квадратите на координати:

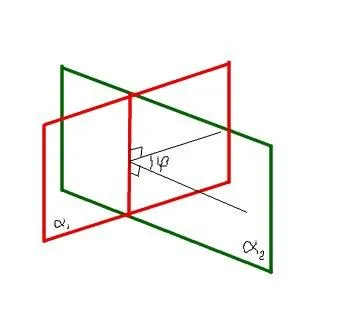
Две пресичащи се плоскости образуват две двойки равни помежду двустенните ъгли. Двустенния ъгъл измерената стойност на съответния линеен ъгъл.

За да се конструира линейна двустенен ъгъл. трябва да се вземат в самолет пресичане на линията произволна точка, а във всеки самолет да прекарат този момент лъча перпендикулярна на линията на пресичане на самолетите. Ъгълът, образуван от тези греди и линейна двустенен ъгъл:

Големината на ъгъла между равнините е количество малък двустенен ъгъл.

Намирането ъгли през скаларна продукта

Ъгълът между векторите

Продукт на вектори и може да се намери чрез сгъване съответните продукти координати на тези вектори:

От дефиницията на скаларното продукта от вектори изразен с формулата

. където е ъгълът между векторите.

Следователно ъгълът между вектори е равен на:

Намерете ъгълът между векторите и

Решение: Ние намери вътрешното произведение на вектори:

= 3 х 4 + 4 + 4 · 0 · 2 = 12 + 16 + 0 = 28.

Нека да вектори модула:

Ние считаме, ъгълът между векторите:

Ъгълът между правите

За изчисляване на ъгъла между две прави линии се използва като вътрешен продукт. Представяме идеята за посока вектор на линията. Ненулеви вектор се нарича посока вектор на права линия L, ако е или директно, L, или по линия, паралелна л.

Нека посока вектори на линии а и б. Ние означаваме с желания ъгъл между тези линии. За решаването на достатъчно проблемът да се намери. тъй като стойността позволява да намерите на ъгъла # 945;.

Представяме нотация: # 1138; ъгълът между тези вектори, след това (ако) или # 945 = 180 ° - (ако # 1138;> 90 °).

Така че един от двамата. един от двамата. Във всеки случай. както и # 945; ≤90 °, след това. и. Ето защо. Като се използва формулата на намиране на ъгъла между векторите, ние получаваме:

Изчислете ъгъла между линии

Водачите насочват векторите имат координати:

Според формулата на ъгъла между правите линии намерят

Ъгълът между правата линия и равнината

Уравнението на равнина е както следва:

В това уравнение, коефициентите на равнина А, В и С - координатите на вектора нормални спрямо равнината (т.е., вектор, перпендикулярна на равнината).

Vector посока вектор линия л. синуса на ъгъла # 946; между линия L и равнината на # 945; е равна на косинуса на ъгъла # 947; между нормалната

() На равнината на указание и директно вектор (. Както

# 946; + # 947 = 90 °, или че е

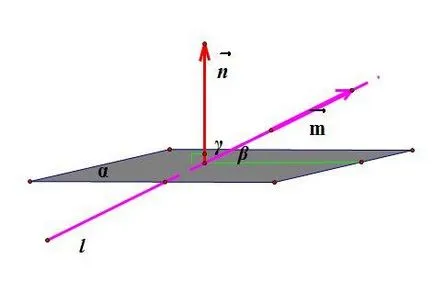
Това е синуса на ъгъла # 946; между права линия, чиято посока вектор и равнината е координати, определени от уравнението

изчислява както следва:

Ъгълът между равнините

Сравняването на самолета. знаейки, координатите на самолета и самолет нормален вектор. Можете да използвате следната формула:

Нека нашият самолет и изчислява по формулата:

косинус на ъгъла # 945; между равнините разположени на следната формула:

В отговор, ние сме на запис. тъй като големината на ъгъла между равнините е ъгъл количеството menshegodvugrannogo. Това означава, че косинус на ъгъла между равнините е косинуса на ъгъла между нормалните на самолетите.

Намерете ъгълът между ploskostyamii

Решение. Заместването във формулата за изчисление на ъгъла между равнините на съответните коефициенти: