Ъглова скорост и ъглово ускорение
Всяко движение на твърдо тяло може да бъде представен като комбинация от транслационни и ротационни движения.
Прогресивно движение - движение, в която всеки ред е твърдо свързана с движещото се тяло, той остава успоредна на първоначалното си положение.
Въртеливото движение - движение, при което всички точки на тялото, които се движат в кръг, чиито центрове лежат на една права линия, наречена ос на въртене.
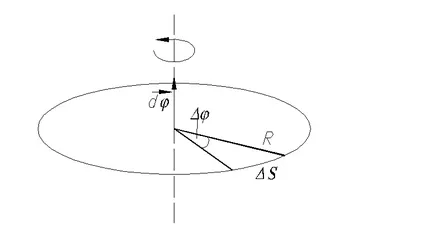
Средната ъгловата скорост


Uglovayaskorost мигновен ъгловата скорост в даден момент в дадена точка на траекторията. Или просто ъгловата скорост



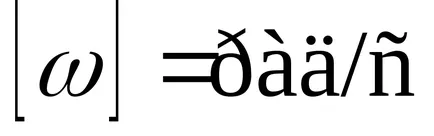
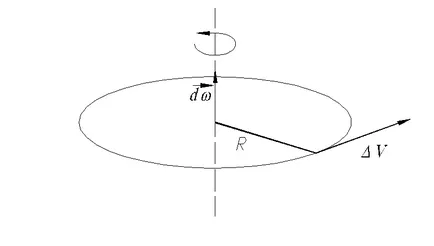
Линейната скорост на точката
,
В вектор форма
линейната скорост на модула |


Ако = конст. въртенето на еднакво и може да се характеризира periodomvrascheniya T - времето, в който момент прави едно пълно завъртане, т.е. върти 2.
t = интервал от време Т съответства на ъгъла на завъртане = 2, тогава
Броят обороти на тялото по време на своето време униформа кръгови движения за единица се нарича скорост.

Средната ъглово ускорение е физическа величина, която е числено равно на съотношението на промяна на ъгловата скорост на интервала от време, през който е настъпила промяната:
Моментната ъглово ускорение или ъгловото ускорение е просто първата производна на ъгловата скорост по отношение на време.
Ускорено вектор на движение


Тангенциална компонент на ускорението, a = d / DT, = R,
Нормалната компонент на ускорение
Връзката между линейни и ъглови стойности са изразени чрез следните формули:
В случай на еднакво ускорени точки за движение по дължината на окръжност ( = конст),
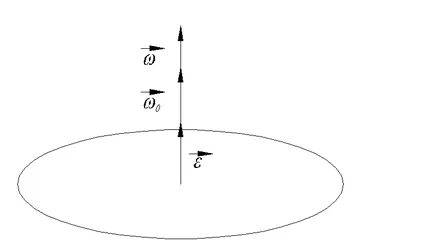
Когато съвпадението на посоката на векторите на ъгловата скорост и ъглово ускорение плюс знак се използва, когато обратната посока - минус.
Основи на динамика.
Сила - този вектор физическа величина характеризиращи взаимодействието на органи.
Взаимодействие на органите, в резултат на което те придобиват ускорението или деформиран, или там е комбинация от двете, наречени сили. Наличието и действието на сили ние можем да кажем:
1. им динамичен проявление, т.е. на ускорението, което го докладва на взаимодействащите тела
2. статичен показ на властта - в деформациите, които се случват в взаимодействащи органи.
В съответствие с двата метода за измерване на силите:
Статичен метод се основава на сравнение на сили от деформации, причинени от тях. Този метод се прилага, когато в качеството сила е пропорционална на напрежението. Той се използва в динамометри.
Динамичен метод се основава на факта, че силата е причината за степента на промяна, т.е. сила - причина ускорение. Установено е, че ускорението на точка е пропорционално на приложената сила. По този начин, сравнявайки ускорението може по този начин за сравнение на силата.
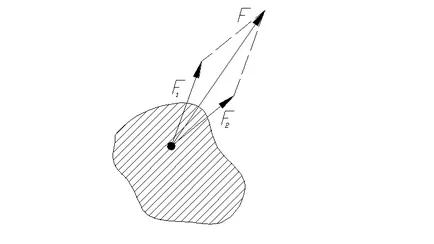
- резултантната на всички сили
В механиката на голямо значение е принципът на наслагване.
