Главна логаритмична идентичност

Главна логаритмична идентичност и логаритъм са тясно свързани.

Главна логаритмична идентичност и логаритъм са тясно свързани. И всъщност, основната логаритмична идентичност е математическа дефиниция на логаритъм на записа. Нека разгледаме по-подробно какво е логаритъм от където са били извършени.

Помислете за алгебрични действия - изчисляване на експонентата х за даден конкретни стойности stepenib и база. Тази задача в общи линии е да се реши uravneniyaa х = б, където А и Б - някои предварително определена стойност, х - неизвестна величина. Имайте предвид, че в този проблем не винаги съществуват решения.

Когато, например, в уравнение х = bchisloa положителен и botritsatelno номер. след това уравнение все още няма корени. Но ако А и Б са положителни и ≠ 1, а след това със сигурност е изключително един корен. Сравнително добре известен фактът, че графиката на експоненциален funktsiiu = а х непременно пресича с pryamoyu = б и, освен това, само една точка. Абсцисата на точката на пресичане и ще бъде в основата на уравнението.

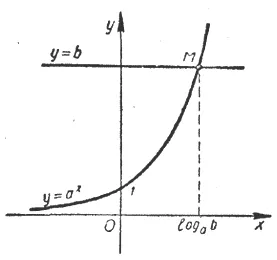
За отбелязване uravneniyaa х = б корен използва Loga б (произнася: логаритъм на б по отношение на основа).

Въз основа на определението, ние получаваме основната логаритмична идентичност:

В следствие на основната логаритмична идентичност е следното правило.

От равенството на две реални логаритми ние получаваме израз логаритъм.

В действителност, когато Loga б = Loga С, при, В = С.

Помислете защо логаритмична идентичности взето лимит> 0, а ≠ 1, б> 0.

Първото условие за ≠ 1.

Добре известно е, че апаратът е степен във всяка единица, и равенство на х = Лога б може да съществува само тогава, когато б = 1. но log1 1 е всяко реално число. За да се избегне тази неяснота и получи ≠ 1.

Обосновете необходимостта от> 0 условия.

Когато = 0 от определението на логаритъм може да съществува само ако б = 0. И тогава следователно log0 0 може да бъде всяко реално число различно от нула. тъй като нулата по всяко различно от нула градуса е нула. Не позволявайте това двусмислие дава състоянието на ≠ 0. Но когато <0 нам бы пришлось отказаться от разбора рациональных и иррациональных значений логарифма. поскольку степень с рациональным и иррациональным показателем определена лишь для положительных оснований. Именно по этой причине и оговорено условие a> 0.

И крайното състояние B> 0 е следствие на неравенство A> 0. защото х = Loga б, и стойността на основата с положителен винаги положителен.