Gibbs фаза правило 1

състояние на системата, в която няколко фази са в равновесие, се нарича хетерогенна. Това равновесие е възможно, ако температурата, налягането и химични потенциали на фази са еднакви.

Нека системата включва K компонент, и тази система е в А - фаза, като в този случай въпросът за броя на независимите параметри, които са необходими за недвусмислено описание на системата, реши да се произнесе, че имам Гибс и която носи неговото име.

Предполагаме, че нашата система е в процес на постоянно налягане и температура, като в този случай условието за равновесие на всеки етап може да се запише като:

където $ F = Н-TS = U + PV-TS $ - Гибс енергия (изобарно - изотермично потенциал), $ _I $ - химически потенциал на компоненти с номер I, $ n_i $ - системни компоненти - концентрация аз. Общият брой на уравнения (1), равен на броя на фазите Общо тези уравнения включва $ (K \ cdot A) $ ценности $ _I $, но не всички от тях са независими. Тъй като съставът на всяка фаза не се променя, тогава има една връзка между химичните потенциали съответно такива условия връзки само (А). Химическите потенциала на всеки компонент във всички фази трябва да са едни и същи, а именно:

За всеки и е А-1 равенство се получава за всички компоненти на К (А-1) състояние. От гореизложеното следва, че броят на независим $ _I $ е:

\ [К \ cdot А-А-К \ наляво (А-1 \ дясно) = К-А \ \ наляво (3 \ дясно). \]

Разбира се, налягането и температурата също са независими параметри. Оказва се, че броят на независимите параметри ($ е $), които са необходими за еднозначно описва система, състояща се от компонент К и се съхраняват в етапите А може да се изписва като:

Припомнете си, че идеален газ, ние описахме използване на два параметъра, например, налягане и температура, и установено от уравнението на състоянието обем. Уравнение (4) се нарича фаза правило Гибс.

В ситуацията, когато равновесието на системата се влияе не само външните параметри като налягане и температура, като, например, електрически полета, магнитни полета и т.н. В този случай, без външни фактори Бюд 2 както в (4), и В (в общия случай), след експресията може да се изписва като:

където В - брой външни независими параметри.

Понякога, например, често го правят в металургията при разглеждане на налягането може да се счита постоянни кондензирани системи, както и влиянието на неговата небрежност, в този случай, като се смята, че фаза правилото за Гибс е писано:

С други думи, може да се каже, че ако всеки от параметрите на външната система е фиксирана (например състоянието р = CONST и Т = CONST), се извършва обикновено във формата на фаза (6).

Изрази (4), (5) и (6) показват, че броят на степените на свобода, не може да е отрицателна, тя няма физически смисъл. От $ е \ GE 0 $, а след това на броя на съществуващите фази система удовлетворява неравенството:

\ [A \ ле К + 2 \ \ наляво (7 \ дясно). \]

В неравенството (7) означава, че броят на фазите, които могат да бъдат в равновесие един с друг не може да надвишава броя на компонентите на повече от две. Това твърдение е друга формулировка на правилото за фаза Гибс.

В една единствена съставка, $ 1 \ ле A \ ле $ 3. Когато $ А = 3, \ е = $ 0, това означава, че трите фази могат да съществуват в равновесие вещество (например, газ, течни и твърди) в само едно състояние, което се нарича тройна точка.

правило Gibbs фаза

Според Гибс се произнесе, че е получена, че с увеличаване на броя на компонентите в системата се увеличава степента на свобода, от друга страна, ако броят на фази на системата се увеличава, намалява броя на необходимите променливи.

Гибс фаза правило се използва в металургията, химическата инженерство, наука. Тя ви позволява да се изчисли броят на фазите в многокомпонентни системи, а броят на термодинамични степени на свобода.

Ако в рамките на многофазни система химически реакции, е необходимо да се вземе предвид броят на химични уравнения. Съставът на тези уравнения ще уравнения, отнасящи се концентрации уравнение материален баланс. Допълнителни уравнения трябва да се изваждат от дясната страна на уравнение (4), или чрез просто като се има предвид броя на компонентите. Използвайте $ K '= K-л $ вместо К, където $ л $ - броят на допълнителни уравнения.

Задача: Определяне на $ А, \ К \ и \ е $ за флуидни системи - това двойки използвайки принципите на Гибс. Как да термодинамични диаграма показва състоянието на такава система?

Тъй като условието, че течната система и пара, броят на наличните фаза - две. Това означава, че А = 2, системата е един от компонентите на К = 1. След това, в съответствие с правило номер Гибс уравнения еднозначно, описващи състоянието на системата ще бъде равен на:

Заместник-подходящите стойности, които получаваме:

Тъй като броят на уравнения, които е необходимо да се описват система е равен на една, след термодинамична диаграма, например в оси (Р, Т) компонент система от две фази е показан като линия АА (фазов преход диаграма течност в пара фиг. 1).

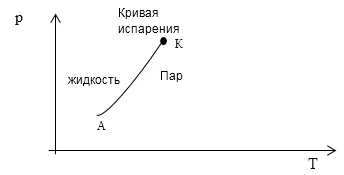
A: $ А = 2, \ к = 1 \ и \ F = 1 $. Състоянието на такава система е показано на диаграмата фаза на кривата на фиг. 1.

Задача: Какъв е броят на степените на свобода на една система на трифазен държава с един компонент. Какво може да се каже за параметрите на такава система в състояние на равновесие?

Според правилото на фазите на Гибс, ние можем да напишете:

Системата има един компонент: К = 1, система за трифазен, което А = 3, броят на необходимите търсене уравнения за правило е Гибс:

Ние извършваме замяната на данни:

Отговор: От $ F = 0 $, това означава, че трите фази на еднокомпонентна система могат да бъдат в равновесие само на едно съотношение на параметрите на системата. Тази точка се нарича тройна на термодинамичен диаграма. Графиката на кривите на тройни точка на топене пресичат, изпаряване, и сублимация.