Геометрични и механични смисъла на производно

С изчисляване на деривата се сблъскваме, когато е необходимо да се определи степента на промяна на един количество - функции в зависимост от промените в другите стойности - независима променлива.

Централните функции на скоростта на промяна в прехода от стойностите на независимата променлива на стойността на функцията съотношение нарастване се нарича до нарастване на независимата променлива, т.е.

Вярно или мигновен скорост на промяна на предназначението на дадена стойност на независимата променлива е границата, до която има тенденция средно изменение на функцията клони към нула нарастване на аргумента:

Механичната смисъла на производно

(Механична смисъла на производно)

Като се има предвид пътя на движение на точка. Скоростта на материал точката от време, е производно на начина, по време:

Задача. Тялото се движи по права линия, съгласно (т). Определя се скоростта му по това време с.

Решение. Желаната скорост - е производно на другото, т.е.

В даден момент от време

Още примери за производни на вземане на решения Online

Геометрична смисъла на производното

Функцията производно, изчислени при дадена стойност, равна на допирателната на ъгъла, образуван от положителната посока и положителната посока на допирателната към графиката на функцията в точката с абсцисата:

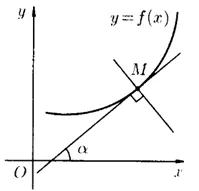
Геометрично производно е наклонът на допирателната към графиката на функцията на точка.

Задача. Фигурата показва графика на №1 и допирателна към него в точката с абсцисата. Намерете стойността на.

Решение. Геометричната смисъла на деривата получаваме, че

Ние намираме ъгъла. Помислете триъгълник - правоъгълна, равнобедрен. След това, така че

И това следва, че

Още примери за производни на вземане на решения Online