Геометричната смисъла на определен интеграл

Комбинирането на тази теорема с разтвора III. Ние виждаме, че криволинеен трапец, в това каза проблем има площ F. и тази област се изразява чрез формулата

Четенето на тази формула прав, ние откриваме

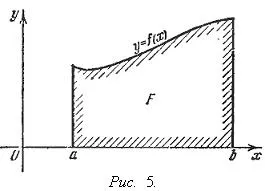
Геометричната смисъла на определен интеграл. Ако е (х) е непрекъсната и положително на [а. Ь], интеграл

Той представлява областта на криволинейна трапец, ограничена от линиите Y = 0, X = а. х = б. Y = е (х) (вж. Фиг. 5.).

Не бива да мислим, че условието за непрекъснатост е необходимо да се гарантира, че тя е съществувала на определен интеграл. Интегралът може да съществува и прекъснати функции. Да предположим, например, F функция (X), определена на интервала [а. Ь], е равна на нула при всички точки на интервала, но ограничен брой точки Z1. z2. Zn. Съставите за е (х) неразделна сума # 963; ,

Нека точките # 958; 0. # 958; 1. # 958; п -1. включени в определението за # 963;. р точки съвпадат с ZI на точки. а останалите са различни от тях. След това, в размер на # 963; р само ще условия различни от нула. Ако повечето от номерата | F (зи) | (I = 1, 2 N) е К. тогава очевидно

когато е ясно, че # 955; → 0 ще # 963; → 0. По този начин, интеграл

Той съществува и е равна на нула.

Сега дам един пример за функция, която не е неразделна. нека # 966; (X) се определя на интервала [0, 1], както следва:

Ако ние, възлизащи на сумата от # 963;. за точка # 958; к изберете ирационално число, тя ще се появи # 963; = 0. Ако всичко # 958; к да вземе рационално, можете да получите # 963; = 1. По този начин, поради простото намаляване # 955; не може да донесе # 963; която и да е броят на постоянните и неразделна

В момента ние знаем точните признаци, че ще разкрият или не функция на определен интеграл даденото, но ние се ограничаваме до горната теорема на integrability на непрекъснатост.

решаване на някои проблеми