функция Селективна дистрибуция

За емпирични случайна величина, като се има предвид емпиричен закон на разпределение, е възможно да се запише и да се изгради на персонализирана функция за разпространение.

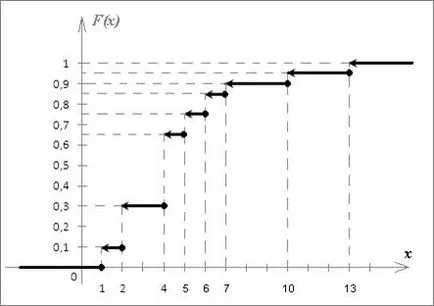
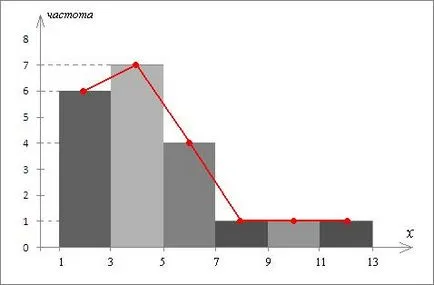
случайна променлива функция дефинирани по цялата реалната ос и определен от уравнението: F (х) = Р (# 958;

Когато х ≤ 1 събитие # 958; 20 <1 невозможно, т.к. нет значений ξ20 меньше 1, а вероятность невозможного события равна нулю, следовательно,

В интервала 1

В интервал 2

В интервала 4

Разликата 5

Така, функцията за селективна дистрибуция е:

Определя се стойността на функцията на разпределение на цялата реалната ос, е възможно да се изгради своя графика (Фигура 1).

График функция селективна дистрибуция има стъпаловидна форма и е конструирана под формата на сегменти: най-малката стойност на ляво (х = 1), стойността на функция е 0 (т.е., една и съща графика с хоризонталната ос); във всяка следваща точка XI състезателна среща при стойност на вероятността # 957; т. .Naprimer в точка x1 = 1 се състезава # 957 = 1. 0.1 (виж емпиричната закона на разпределение.); в точка х2 = 2 се състезава # 957; 2 = 0.2; в точка x3 = 4 се състезава # 957; 3 = 0.2; и т.н. Вдясно от най-високата стойност (х 8 = 13), функцията е равен на единица. Стрелките на краищата на точките на сегменти показват, че функцията е определена на интервалите.

С са групирани голям обем извадка от неговите елементи. За този интервал, съдържащ всички примерни стойности (от xmin да Xmax), се разпределя в m несвързани интервала. Предполага се, че дясната граница интервал принадлежи на следващия интервал (последния интервал съдържа както своите граници). Броят на интервали т могат да бъдат избрани произволно, или да намерят формула Стърджис:

където п - размер на пробата.

Тогава дължината на всеки интервал е равен. където w - вземане на проби обхват.

След това, честотата брои Ню Джърси - брой на пробите, принадлежащи към к-ти интервал, както и натрупаната честота. Резултатите са както групирани честота проба. Процесът на формиране на такава маса с честота се нарича раздел.

Начертайте честота раздела вземане на проби от нашия пример.

Ние дефинираме броя на интервали Стърджис с формулата:

Броят м трябва да бъде цяло число, т.е. или 5 или 6. Тъй педя проба равни. това е по-удобно да m = 6, защото В този случай, продължителността на един интервал. Ако вземем m = 5, а след това. което не е много удобно, защото Примерни стойности са цели числа.

По този начин, разделяне стойностите на интервал за вземане на проби (1 до 13) на интервали в стъпки. Резултатите се записват в таблица (таблица 1).

В първия слот брой колона запис на от 1 до 6. След това, с помощта на случайни числа за вземане на проби интервали определят граници и да ги пишат във втората колона:

1) най-малката стойност проба е 1, тогава ние започваме да се изгради 1:

1 + 1 → 3 → 2 = 3;

2) 3 → 3 + 2 = 5 → до 5;

3) от 5 → 5 + 2 = 7 → 7;

4) 7 → 7 + 2 = 9 → до 9;

5) 9 → 9 + 2 = 11 → 11;

6) 11 → 11 + 2 = 13 → 13.

Най-голямата стойност проба е 13, това означава, че интервалите са определени правилно.

В третата колона, пише в средата на интервалите получени. Средният интервал (а, б) може да се намери с формула :. например, за 1-ти интервал; за втория интервал и т.н.

четвъртата колона запис честотен интервал, т.е. честота проникване на проби в интервала, например:

в първи спад интервал стойности 1 и 2, със стойност 1 2 пъти отговаря (n1 = 2) [15]. стойност 2 възниква 4 пъти (N2 = 4), така че първият интервал честота е равна; първи запис линия 6;

в продължение на 2 минути интервал стойности попадат 3 и 4, където стойността 3 не се среща в пробата, на стойност от 4 е намерена 7 пъти (n3 = 7), така че вторият интервал честота е равна; втори запис линия 7;

3-ти интервал стойности попадат 5 и 6, където стойността 2 открити 5 пъти (n4 = 2), стойността 6 е намерена като 2 пъти (n4 = 2), така че третият честота е равна на интервал; трета запис линия 4 и т.н.

Петата колона на Таблица 1 запис кумулативните честоти на принципа: -ти chastotanakopl й. =. (J - 1) -ти chastotanakopl + J тата chastotaint. Например:

Първа съхранява честота е 6, защото предишния кумулативна честота е равна на 0 (не е) и първия интервал честота е равна на 6 (виж четвърта колона.): 0 + 6 = 6;

Второ кумулативна честота е равна на 13, като предишна (I-1) кумулативна честота е 6, и втора честота интервал равна на 7 (виж четвъртата колона.): 6 + 7 = 13;

Трето кумулативна честота е равна на 17, като предишна (2) кумулативна честота е 13, а третият интервал честота е 4 (виж четвърта колона.): 13 + 4 = 17 и т.н.

В тази извадка раздела честота свършва.

номер вариация може да бъде представен графично и чрез изграждане на полигон и вземане на проби хистограма честота. Графично изображение проба за визуално оценяване разпределението на плътността на вероятността на населението.

За конструиране на многоъгълника и хистограмата проби в този пример, използването на данните в съответствие с таблица 1.

На координатната равнина на хоризонталната ос представя примерни стойности (XI), като вертикалната ос - честота (Ni) (фиг.2). Отделните сегменти на оси могат да бъдат различни (техния размер е избран, принципът на яснота).

Хистограма. На интервали равни интервали от Таблица 1 (втората колона), правоъгълници са конструирани с височина, равна на честотата на интервал съответстващ (четвъртия колона на Таблица 1). Полученото набор от правоъгълници, наречени хистограма проба.

Polygon. Свържете средата на горната страна на правоъгълници хистограмата. Получената полилинията се нарича земята проба (на фигура 2 е посочено в червено).

Тестване на хипотезата за закона за разпределение

Помислете за процеса на тестване на хипотезата за закона за разпределение в примера в предишния раздел.

Пример. В книгата "Мечо Пух и всички всички всички" отворени за произволна страница, където можете да изберете произволна дума. В този случай, фиксираната дължина на думата. Като резултат от 20 тестове на следващата проба се получава:

4, 1, 4, 5, 1, 13, 4, 10, 2, 4, 7, 2, 2, 4, 6, 4, 5, 6, 2, 4.

1) Изчислява примерни характеристики: средна проба, вариацията проба, обективна оценка на вариацията.

2) Когато нивото на значимост # 945; = 0,05 за тестване на хипотезата, че дължината на думата нормално разпределение. Параметрите на разпространение се оценява на базата на проба: очаквания - от средната проби, стандартно отклонение - на квадратния корен на обективна оценка на вариацията.

средната стойност на пробата може да се намери с формула

където К - брой на различните примерни единици,

п - размер на пробата.

Обективна оценка на дисперсията:

Обикновено характеристики примерни процес изчисление форма под формата на таблица (Таблица 2).

В нашия пример, к = 8, п = 20, в XI стойности и Ni са показани в броя на статистическата проба. Попълване на маса селище започнем да попълваме XI и никелови колони. записването им в редица статистически данни. Тогава ние се изчисли продукт на XI · Ni и резултатите се записват в третата колона. Последният ред обобщи получените 90. Сега се изчисли средната проба данните. разделяне на получената сумата от обема на пробата, т.е. 20.

Сега, изчисляване на средната проба, попълнете четвъртата колона, запис в нея, отговаряща на разликата. например:

Пишем на първа линия на -3.5;

Пишем втория ред -2,5 т.н.

В петата колона, предишната колона напишете квадратите на ценности, като например:

Пишем първата линия 12.25;

Пишем на втора линия 6.25 и т.н.

След това, ние се размножават стойностите, получени за петата колона на подходящата честота (втората колона) и резултатът се записва в последната колона, като например:

Пишем първата линия 24.50;

Добави 25,00 на втория ред и т.н.

Последният ред на последната колона обобщава получените данни 165.00. Сега ние се изчисли дисперсията на извадката:

Ние считаме, обективна оценка на вариантите, знаейки, дисперсията на извадката: