функция на Лаплас

Пример 2 Непрекъснат случайна променлива X има нормално разпределение със следните параметри: m = 3,  = 4. Виж вероятността, че резултатите от теста и случайна променлива X.) приема стойност в интервала (2; 6); б) има стойност, по-малка от 2; в) да заема стойност по-голяма от 10; г) се отклонява от очаквания с размер не повече от 2 графично илюстриране на разтвора.

Решение. а) вероятността нормална случайна променлива X попада в предварително определен интервал (, ), където  =  = 2 и 6, е равна на:

б) вероятността нормална случайна променлива X заема стойност по-малка от 2, е:

в) вероятността нормална случайна променлива X ще се стойност по-голяма от 10, е равна на:

ж) вероятността нормална случайна променлива X отклонява от очакването, с по-малко  = 2, е:

От геометрична гледна точка, изчислената вероятността е числено равно на защрихованата област под нормалната крива (вж. Фигура 6).

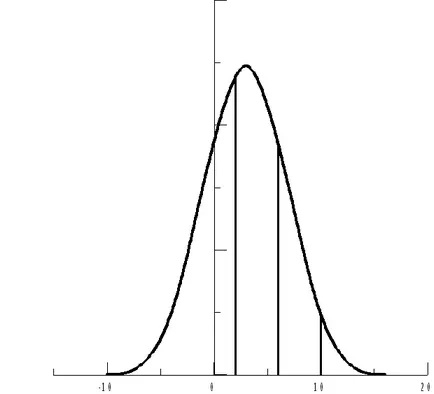
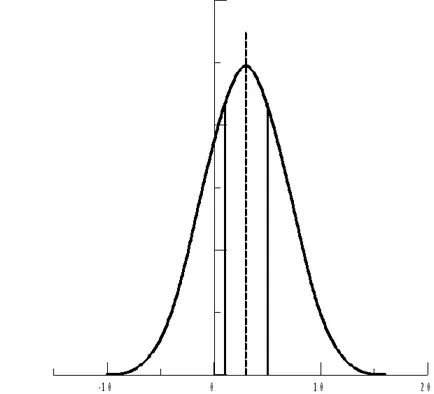
Фиг. 6. нормалната крива за случайна променлива X

Пример 3 Произведени измерване диаметъра на вала без систематични (един знак) грешки. Случайни грешки измерване подлежат на нормално разпределение със стандартно отклонение от 10 мм. Намерете вероятността, че измерването е направено с грешка не по-голяма в абсолютна стойност от 15 мм.

Решение. Очакванията на случайната грешка е нула т = 0. След това вероятността, че нормално случайна променлива X ще се отклонява от очакването, с по-малко  = 15, равно на:

Пример 4. Машината произвежда зърна. Топката се счита за добре, ако отклонение X от диаметъра на топката от големината на проектиране на абсолютната стойност на по-малко от 0.7 mm. Ако приемем, че случайна променлива X е нормално разпределена със стандартно отклонение от 0.4 mm, се намери средния брой на топки ще се поберат между 100 произведени.

Решение. В случайна променлива X - отклонение на диаметъра на топката от размера на проектиране. Очакванията на отклонение е нула, т.е. М (X) = m = 0. След това вероятността, че нормално случайна променлива X отклонява от очакването, с по-малко  = 0,7, е равна на:

Това означава, че около 92 на сто топката ще се побере.

Пример 5 За да докаже правилото "3 ».

Решение. Вероятността, че нормално случайна променлива X отклонява от очакването, с по-малко  = 3 . е равна на:

Пример 6. случайна променлива X е разпределена обикновено със среден т = 10. Вероятността от удари X в интервала (10, 20) е равно на 0.3. Какво е вероятността за получаване на X в интервала (0, 10)?

Решение. Нормалната кривата е симетрична спрямо линия х = M = 10, така че зоната, ограничена по-горе и по-долу нормалните интервали кривата (0, 10) и (10, 20) са равни. От областта на контакт с вероятностите са числено равно на съответния интервал X, тогава: