Функциите на прехвърлянето на отворени и затворени системи - studopediya

функцията за трансфер на отворения контур (фигура 7.1.):

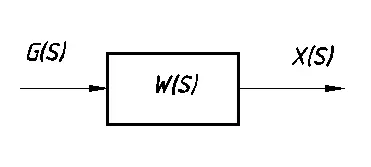
Забележка: Устройството се нарича интегриране, ако знаменателят е чиста S; ако S в чиста форма е в числителя, връзката се нарича диференциатор.

Системата за диференциално уравнение под формата на L:

Функцията за прехвърляне на системата в единици последователно свързване (виж фигура 7.2 ..):

Функцията за прехвърляне на системата в паралелно свързване единици (виж Фигура 7.3 ..):

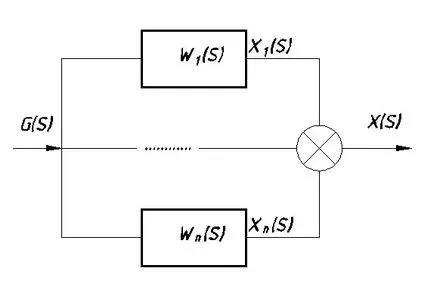
Местна обратна връзка:

Системата за уравнение с обратна връзка (виж Фигура 7.4 ..):

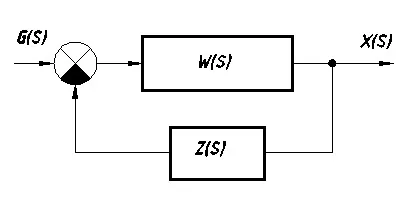
Когато устройството за обратна връзка:

Забележка:-нататък W (S) е предавателната функция на отворен контур, F (S) е предавателната функция на затворената система. Функцията за прехвърляне на затворена система:

Характерните полином на затворена система:

Характерните уравнението на затворената система:

Характерните уравнението на отворената система:

функцията за трансфер на смущението от:

Разглеждане на системата, показана на фиг. 7.5.

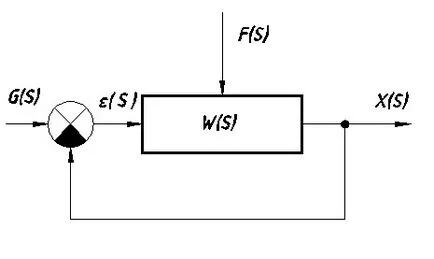
· # 949 (т) / # 949; (S) -error

Функцията за прехвърляне на грешката:

Трансформирайте първоначалната схема с правилата на структурните реформи (виж Фигура 7.6 ..):

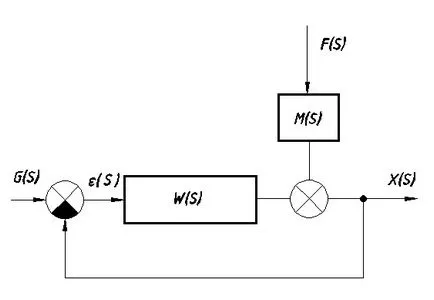
Следователно, функцията за трансфер на смущението от IS:

Забележка: Редът на отворената система, се определя по реда на затворена система.

Основните уравнения на системи за проследяване.

В диференциално уравнение на системата (виж Ris.7.6.):

В диференциално уравнение на затворена система:

диференциално уравнение за отклонението на грешка:

Системата за диференциално уравнение под формата на Cauchy и без да се нарушава входните действия:

Това уравнение определя подходящото движението на системата

Характерните уравнението за контрол:

. където Е - матрица идентичност