фаза и група скоростта на светлината на

Тъй като индексът на пречупване и следователно скоростта на светлината зависи от честотата и светлина не строго едноцветен, възниква въпросът за това, което се разбира от скоростта на разпространение на светлинния сигнал измерени експериментално.

Всички приемници реагират на светлинна енергия, така че във всички експерименти на скоростта на предаване на енергия се измерва чрез светлинен сигнал; той се нарича скорост на групата и. Тя се различава - от скоростта на размножаване фаза (фаза скорост) νφ, който е чисто определя от изчислената стойност и реалната част на индекса на пречупване. Далеч от двете скорост дисперсия област почти съвпада.

За изясняването на тези понятия, помислете за две вълни, които имат еднаква амплитуда и относително близки честоти:

Сега нека си представим, движещ се с вълните и да го гледате в една и съща фаза на наблюдател. За тази наблюдател при следното условие:

и скоростта му е равна на скоростта фаза на вълна,

Ако друг наблюдател ще се премести заедно с максимално "вълна група" амплитуда (.. Т.е. максималната енергия), при следното условие за него:

и скорост (група) е

Отбелязва, че между производното на брой вълна к и производното с дължина на вълната (в средата) съществува връзка:

ние получаваме връзката между групата и фаза скорост:

Следователно, скоростта на група може да съвпада с фазата (без дисперсия), е по-малко от фаза (нормална дисперсия) или по-голяма от (в аномална дисперсия). Въпреки това, можем да покажем, че в съответствие с теорията на относителността група скорост никога не превишава скоростта на светлината във вакуум:

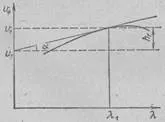
Трябва да отбележим, че в заключение, че в силна дисперсия на понятието група и фаза скорости не са достатъчни за правилното описание - разпространение на вълните. Но ние няма да се ангажират с по-нататъшно усъвършенстване. P. Ehrenfest предложен елегантен начин за намиране на скоростта на група. Познаването на хода на индекса на пречупване п = F (λ). може да се конструира крива νf = F (λ) (фиг. 8.3). Като допирателна към кривата в точката с координата λ1. Ние определяме пресечната ос тангента на ордината равна на стойността на скоростта на група в близост до λ1 на вълната. u1 = ν1-h1 (вж. Eq 8.8).

Молекулите (или атоми) диелектрици под въздействието на електромагнитно поле вълна

посадъчен в диелектрика скоростта на светлината, пристигат в принудени трептения и се превърне вторични радиатори на вълни, а съгласувани с основната вълна (8.9), но изместен във фаза. В допълнение към основната вълна, тези вълни произвеждат нова вълна, фазата на който също е различно от фазата на основната вълна - това може да се тълкува като разпространението на вълната сума със скорост фаза, различна от С.

Ако вълната пътува в диелектрик път л със скорост където тя прекарва времето си

Ако вълна е преминала същия път във вакуум със скорост с, изминалото време ще бъде равна на t2 = л / гр. Следователно, разликата във времето е равна на:

Ако периодът на вълната, равна на T изоставането фаза ще бъде:

Ние показваме как в най-простия случай може да се разгледа влиянието на вторичните вълни. Да приемем, че плоска вълна (8.9), простиращ се по посока на увеличаване на х, срещне по пътя на плосък диелектричен слой, неговите страни имат координати (х = 0 и АН). Намираме напрегнатостта на полето в точка А на координати (х = А у = 0, Z = 0), където А >> λ. Тази област се състои от областта на вълната (8.9) и допълнително поле, създадено от диполи на диелектрик, т. Е.

За да се изчисли ЛЕ използват метода на Френел зони (§4.1). Полето в точка А се определя от действието на половината от първата Fresnel зона; е окръжност с център в основата, върху която е конуса на лъчи, идващи от различни точки на зоната и конвергенция в точка А. Дължините на тези греди са променени от А до А + λ / 2. Очевидно радиус зона е

Площ зона е S = πρ 2. Обем на диелектрик цилиндър, лежи на тази зона е равна на ΔV = S АН. Когато концентрацията на молекули N брой молекули на обем е показан ΔN-N ΔV.

молекули придобиват диполни моменти р Под влияние на областта на вълната (8.9). Напрежението дипол радиация поле в екваториалната равнина на разстояние R е равна на:

Тъй като размерът на ъгъла област е много малък, може да се предположи, че всички диполи излъчват своя екваториална равнина. R Разстоянието в знаменателя на (8.12) може да се приема като А. същите аргументи могат да средното разстояние:

? Тогава силата на полето, създадено в точка А всички обема на диполи V, е равна на:

Ако я добавите към интензивността на фундаменталната вълна на областта, получаваме:

Тъй като (поради обема е малък), а след това можете да вземете:

По този начин, забавяне фаза е равна на:

Но, както е добре известно (вж. "Електрически и магнитни измервания», § 1.9),

Ние не се вземат под внимание взаимодействието на диполи една с друга, която е допустима само при ниски концентрации на молекули, т.е.. Е. За газове. Но в същото време н почти не се различава от единство, и може да бъде взето

Следователно, (8.15) следва крайния израз за преминаването фаза:

Този израз се различава от точната израза (8.10) само с фактор π / 2 близо до единица. Появата на този фактор обяснява опростена изчислението (това е необходимо, за да се интегрират полеви диполи, а ние се средната стойност и се умножава по броя на диполи).

По този начин, механизмът за забавяне, описани по-горе са довели до истински оценка на преминаването фаза.