Естествени числа, уравнение

Задача. От лявата чаши теглата са диня и тегло от 2 кг, а от дясната чашка - тегло 5 кг. Везни са в равновесие (фиг. 37). Каква е масата на динята?

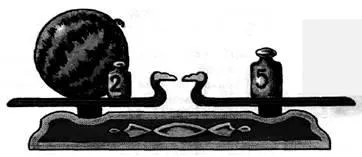
Фиг. 37. Балансът в равновесие

Решение. Означаваме неизвестен масата на диня с буквите х. Тъй като балансът е в равновесие, равенството х + 2 = 5.

Ние трябва да се намери стойност на х. за които това равенство. По смисъла на тази стойност изваждане е разликата на номера 2 и 5, т.е. 3. Следователно, диня тегло е 3 кг. Добави: х = 3.

Ако равенство включва писмото, уравнението може да е вярно за някои стойности на буквите и наред с другите си значения.

Например, уравнение х + 2 = 5 е валидна за х = 3, и когато X е невярно = 4.

Уравнението се нарича уравнение, съдържаща буквата, чиято стойност трябва да бъде намерен.

Значение на писма, в която уравнението се получава от правилната числено равенство, се нарича корен на уравнението. (Например, корена на уравнението х + 2 = 5 е броят 3.)

Решете уравнението - това означава да намерите всички своите корени (или да сте сигурни, че това уравнение не разполага с един-единствен корен).

ПРИМЕР 1 Нека решаване на уравнение х + 12 = 78.

Решение. По смисъла на изваждане неизвестен срок е равен на разликата между сумата, а другия план.

Следователно х = 78-12, т.е., х = 66.

Броят 66 е корен на уравнението х + 12 = 78, тъй като 66 + 12 = 78 (фиг. 38).

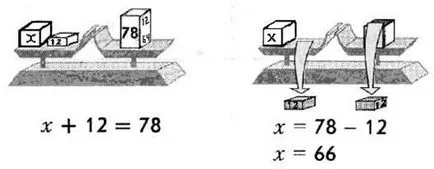
Фиг. 38. Везни и уравнение

За неизвестно термин, е необходимо да се приспада от размера на добре познати Терминът (фиг. 40, както и).

Пример 2. Да решаване на уравнението у - 8 = 11 (Фигура 39)..

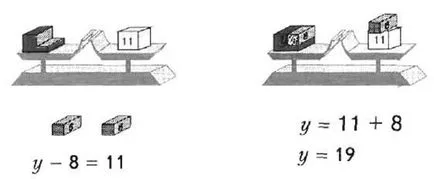
Фиг. 39. Баланс и уравнения

Решение. Чрез изваждане на смисъла, в сумата от номера 11 и 8. След това, у = 11 + 8, който е у = 19.

Броят 19 е корен на уравнението у - 8 = 11, като равенството 19 - 8 = 11.

За да намерите неизвестното е намалено, то е необходимо да се определят умалителят и разликата (фиг. 40, б).

Фиг. 40. Разтворът на уравнения

ПРИМЕР 3 Нека решаване на уравнение 15 - Z = 9.

Решение. Чрез изваждане на смисъла на номер 15 е сумата от Z и 9, т.е. Z + 9 = 15. От това уравнение неизвестната Терминът: Z = 15-9, т.е. Z = 6

Брой 6 е корен на 15 - на Z = 9, тъй като равенството 15 - 6 = 9.

За да намерите неизвестното изважда, че е необходимо да се изважда разликата от намалената (фиг. 40, буква в).

Когато четете уравнения и алгебрични изрази, не забравяйте, че имената на буквите X, Y, Z е мъжествен, както и имената на останалата част от латински букви среден род.

Vail имената на буквите в математиката не е приет.

х + 25 = 50 - сумата от X и е равен на двадесет и пет и петдесет;

х = 25 - X е равен на двадесет и пет;

р - 18 = 20 - рН разлика е двадесет и осемнадесет;

р = 38 - рН равно на тридесет и осем.

Немски учен Карл Гаус (фиг. 41), се нарича цар математици. Неговата математически талант вече е очевидно в детството си. Говори се, че на три години той изненада другите, за адаптиране на изчисляването на баща му и зидари. Един ден в училище (Гаус по това време е на 10 години) учител предложи на класа, за да добавите всички числа от 1 до 100. Докато се диктува задачата Гаус е готова да отговори. На черната дъска е написано: 101 х 50 = 5050.

Фиг. 41. Карл Гаус (1777-1855)

Опитайте сами да се досетите, като Карл Гаус добавя номера от 1 до 100.

В днешно време почти предвид всички народи са десетки, стотици, хиляди, което е десетична бройна система.

В него, както вече знаете, стойността на номера зависи от местоположението (позиция), че е необходимо да се напише номера. Ето защо, една такава система за номериране нарича позициониране.

Преди това, някои хора използват други сметки на системата. В топлите страни от Африка и Америка, където хората отиват боси, по сметката се използва не само с пръсти, но пръстите на краката. Получен от двайсет и няколко години.

Но преди пет хиляди години в някои източноевропейски страни се използва шестдесетичната система номер, т.е. корен 60. Тази система е първата система за позициониране.

Фиг. 42 показва как системата изглеждаше като някои рекордни стойности.

Фиг. 42. Запис на определени номера в шестдесетичната система на номерация на древния Изток

Следи от шестдесетичната все още остават: ние сега се разделят часа в 60-та минута, а след минута - 60 секунди.

Използването на броя 10 като корен се дължи на факта, че хората имат по ръцете си 10 пръста, че е най-добре да се използва с резултата. Но корен, разбира се, може да бъде всяко число. Например, съвременните компютри (електронни компютри) смятат, че в двоичен (База 2), тъй като в този случай само две състояния: "има сигнал" и "няма сигнал".