Цилиндрите от втори ред

а) елиптичен цилиндър

Уравнение (14) не съдържа променлива. В уравнението на равнината (14) определя елипса с полуоси и. Ако точката се намира на тази елипса, а след това във всяка точка на повърхността (14). Наборът от тези точки има повърхност, описан от линия, паралелна направо към оста и пресичащи елипсата

Елипса (14), наречена употреба линия на повърхността, и всички възможни позиции на споменатите движи права - генератори.

Обикновено повърхността описан от права линия, остава успоредна на някои дадена посока и пресича тази линия се нарича цилиндрична. Повърхността (14) е показано в Fig.49.

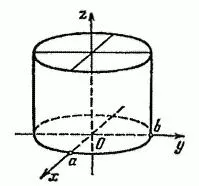
б) хиперболичен и параболични цилиндри

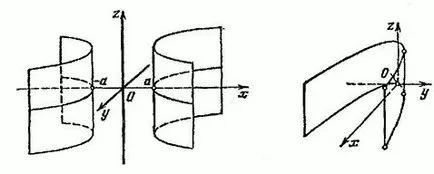
В този случай направляващите повърхнини са хипербола линии и парабола генератори и - директно паралелно ос и преминаване през хипербола или парабола равнина. Повърхността (15) и (16) са показани на Фиг. 50 и 51.

в) паралелно и пресичащи се плоскости. Direct.

За повърхност (17) ръководства са прави линии

Следователно, повърхността (17) има двойка пресичащи се плоскости. В Уравнение повърхности (18) и (19) са в района на двете координати. Уравнение (18) в равнината има двойка от линии.

Ако вземем такива, и след това точките ще задоволят уравнението (18), така че на повърхността (18) има двойка успоредни равнини.

Уравнение (19) описва равнина, като това уравнение е изпълнено, всякакъв вид на точки, и всички от множество, което е равнина.

Може ли да се разглежда и като водач във всеки един от самолетите, или като генератори са прави успоредни на оста или ос и преминаващи през линията.

Уравнение (20) отговаря всеки един момент и с всеки. Следователно (20) представлява права линия, а именно, на оста.