Четириъгълна пирамида в проблем с2
Решаването на проблема на C2 от координиране, много студенти са изправени пред същия проблем. Те не могат да изчисли координатите на точките. във формула скаларен продукт. Най-голямата трудност е пирамидата. И ако на мястото на основата се считат за повече или по-нормално, а след това в началото - истински ад.
Днес ние ще се занимава редовно четириъгълна пирамида. Има триъгълна пирамида (известен още като - тетраедър). Това е по-сложна конструкция, така, че отделен урок ще бъде посветена на него.
Да започнем с това ние си спомняме определението:
Редовен пирамида - това е като пирамида, в която:
- В основата е правилен многоъгълник. Триъгълник, квадрат и др;
- Височина, която се проведе на земята, минава през центъра му.
По-специално, базата е квадратна четириъгълна пирамида. Точно като Хеопс, само малко по-малък.
Равнение на пирамидата, в която всички ръбове са равни на 1. Ако проблемът ви не е така, изчисленията не се променят - просто броя ще бъде различен.
В горната част на четириъгълна пирамида
Така че, предполагам, че са дадени от дясната четириъгълна пирамида SABCD. където S - отгоре, отдолу ABCD - квадрат. Всички ръбове са 1. Трябва да въведете координатна система и да намерят координатите на всички точки. В момента има:
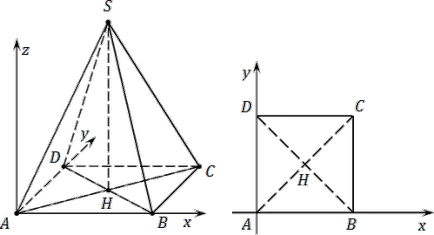
Въведете координатна система с неговия произход в точка А.
- OX ос е успоредна на ръба AB;
- OY ос - успоредна на АД. От ABCD - квадрат, AB ⊥ АД;
- Накрая, OZ ос е насочена нагоре, перпендикулярна на равнината на ABCD.
Сега ние считаме, координатите. Допълнителна сграда: SH - височина, която се проведе на земята. За удобство, ние ще представим на основата на пирамидата на отделен чертеж. Тъй като точка А. Б. С и D лежат в равнина Окси. им координира г = 0. В момента има:
- А = (0, 0, 0) - е произходът;
- В = (1, 0, 0) - етап 1 OX ос от произхода;
- С = (1, 1, 0) - етап 1 на говедото на ос и оста OY 1;
- D = (0, 1, 0) - Стъпка само OY ос.
- Н = (0,5; 0,5; 0) - В центъра на квадрата, средния сегмент AC.
Остава да намерите координатите на точка S. Имайте предвид, че X и Y координатите на точките S и Н са еднакви, тъй като те лежат на една линия, паралелна на оста OZ. Остава да намерите Z координира за точката С.
Помислете триъгълници пепел и ABH.
- AS = AB = 1 състояние;
- Ъгъл AHS = AHB = 90 °, тъй като SH - височина и AH ⊥ HB като диагонала на квадрата;
- Side AH - общо.
Следователно, правоъгълни триъгълници ABH и ASH са на един крак и хипотенуза. Следователно, SH = BH = 0,5 · BD. Но BD - диагонал на квадрат със страна 1. Ето защо, ние трябва:
Общо координати на точката С.
В заключение, пишем координатите на всички върхове на правилна правоъгълна пирамида:
Какво да правите, когато друг перка
Какво става, ако страничните ръбове на пирамидата не са равни на ръбовете на основата? В този случай, помислете за AHS триъгълника.
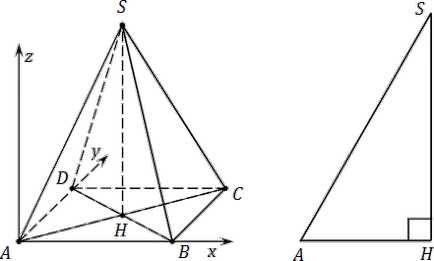
Триъгълник AHS - правоъгълна. и хипотенузата AS - е едновременно страничен ръб SABCD оригиналната пирамида. AH крак лесно смята: AH = 0,5 · AC. Останалите SH В крак намерите питагорова теорема. Това ще Z координира за точката С.
Задача. Дана редовен четириъгълна пирамида SABCD. в основата на който е квадрат със страна 1. страничен ръб BS = 3. Откриване на координатите на точка S.
X и Y координатите на точките, които вече знаем: х = Y = 0,5. Това следва от два факта:
- Проекцията на точка S в равнина Окси - точка е Н;
- В същото време, буква З - ABCD центъра на площада. всички от които са страни 1.
Остава да се намери точката на координиране S. Помислете AHS триъгълник. Това е правоъгълна, хипотенузата AS = BS = 3 катет AH - половината диагонално. За допълнителни изчисления, ние се нуждаем дължина:
Питагорова теорема за триъгълник AHS. AH 2 + 2 = SH КАТО 2. Ние имаме:
По този начин, координатите на точката С.
- Безплатна Подготовка за изпита 7 прости, но много полезни уроци + домашна работа
