Бернули

Ние няма да говорим за дългосрочните - ще започне незабавно с определение.

Схема Бернули - когато п е направен от същия тип независими експеримента, всеки от които могат да получават събитие от интерес за нас А. и известна вероятност за това събитие P (A) = р. Необходимо е да се определи вероятността, че по време на изпитанията на п случай, че се появи точно к пъти.

Проблемите, които се решават от схемата на Бернули, са изключително разнообразни: от прости (като "намери вероятността, че стрелецът удари едно време от 10") до много тежка (например, проблемът на лихвите или карти за игра). В действителност, тази схема често се използва за решаване на проблеми, свързани с контрола на качеството на продукта и надеждността на различни механизми, като всички те трябва да бъдат известни преди започване на работа.

Да се върнем на определението. Тъй като ние говорим за независими проучвания, във всеки експеримент, вероятността на събитието А е един и същ, само два възможни изхода:

А - настъпване на събитие А с вероятност р;
"Не" - събитие А не изглежда, че се случва с вероятност р = 1 - стр.

Най-важното условие, без което Бернули схемата губи значението си - това постоянство. Без значение колко експерименти ние не се извършва, ние се интересуваме от едно и също събитие, А., която се проявява със същата вероятност стр.

Между другото, не всички проблеми в теорията на вероятностите са намалени до постоянни условия. Това ще ви каже всеки компетентен учител по висша математика. Дори и толкова проста достатъчно нещо като извади цветните топки от кутията, а не с постоянни условия. Те извади друга топка - съотношението на цветове в кутията се е променило. Следователно, ние променихме и вероятност.

Ако условията са постоянни, е възможно да се определи точно вероятността дадено събитие А се случва точно к пъти от възможни п. Нека да формулира този факт като теорема:

теорема на Бернули. Нека вероятността от настъпване на събитие при всяко проучване е постоянна и равна на стр. Тогава вероятността н независими изпитвания на събитие се появява точно к пъти, се изчислява, както следва:

където С п к - брой комбинации, р = 1 - стр.

Тази формула се нарича: Бернули формула. Интересно е да се отбележи, че задачите, изброени по-долу, се решават без използването на тази формула. Например, ние може да се приложи формула добавяне на вероятности. Въпреки това, размерът на изчисление е просто нереалистично.

Задача. Освободете вероятността от дефектни продукти на машината е 0.2. Определете вероятността, че серия от десет издадени на тази машина точно к части са без брак. За решаване на проблема за к = 0, 1, 10.

По предположение, ни интересува в случай освобождаване на продукти без брак, което се случва, всеки път с вероятност р = 1 - 0.2 = 0.8. Необходимо е да се определи вероятността дадено събитие да се случи к пъти. Събитие А контрастира със събитието "не А», т.е. издаване на дефектни продукти.

По този начин, ние имаме: п = 10; р = 0,8; Q = 0,2.

Така че, намери вероятността, че всички части дефектна (к = 0), че е само едно парче без брак (к = 1), както и че дефектните части не на всички (к = 10) в играта:

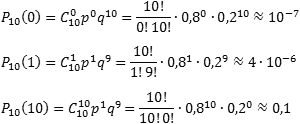
Задача. Coin хвърли 6 пъти. Глави и опашки с еднаква вероятност. Намерете вероятността, че:

герб ще падне три пъти;
герб ще падне веднъж;
герб ще падне най-малко два пъти.

Така че, ние сме заинтересовани в случай, когато А. герб пада. Вероятността от това събитие е р = 0,5. А контрастира събитие събитие "не", когато попада опашки че настъпва с вероятност р = 1 - 0.5 = 0.5. Необходимо е да се определи вероятността герб ще падне к пъти.

По този начин, ние имаме: п = 6; р = 0,5; Q = 0,5.

Определете вероятността, че гербът падна три пъти, т.е. к = 3:

Сега ние определяме вероятността, че палтото е паднал само веднъж, т.е. к = 1:

Остава да се определи каква е вероятността герб падне най-малко два пъти. Основната трудност - във фразата "най-малко". Оказва се, че ние ще организираме всеки к. освен 0 и 1, т.е. количеството, необходимо да намерите стойност X = P 6 (2) + P 6 (3) +. P + 6 (6).

Забележете, че това количество е равна на (1 - P 6 (0) - P 6 (1)), т.е. достатъчно на всички възможни варианти "рязани" тези, където герба падна 1 пъти (к = 1), или не е спаднала изобщо (к = 0). Тъй като P 6 (1), което вече знаем, че е необходимо да се намери P 6 (0):

Задача. Вероятността, че телевизорът е скрил дефекти е 0.2. В склада получи 20 телевизии. Каква е вероятността на дадено събитие: че в тази игра там са два телевизора със скрити дефекти или три?

Събитие на интереси A - наличието на скрит дефект. Общо п = 20 телевизори, латентна дефект вероятност р = 0,2. Следователно, вероятността да се получат телевизия без латентна дефект е р = 1 - 0.2 = 0.8.

Получават се излиза условия за Бернули схема: п = 20; р = 0,2; Q = 0,8.

Нека да намерим вероятността за получаване на две "дефектен" на телевизора (к = 2) и три (к = 3);

Очевидно, Р 20 (3)> P 20 (2), т.е. вероятността за получаване на три телевизора с скрити дефекти по-вероятно да се получи само две от телевизора. Освен това, разликата не е слаб.

Една малка забележка за факториелите. Много хора имат смътна чувство на дискомфорт, когато видят цифрата "0" (да се чете "нула факториел"). Така че, 0! = 1 по дефиниция.

П. С. Но най-голямата вероятност през последната задача - е да се получи четири от телевизора чрез скрити дефекти. Математика - и се уверете.

Безплатна Подготовка за изпита 7 прости, но много полезни уроци + домашна работа