Бележки programmistera интелигентни системи

Ежедневната работа на съвременния програмист рядко оставя място за развитие на творческото мислене. По-често, отколкото не, за решаване на проблемите, е достатъчно да се прилага доказано решение: модел или библиотеката. Познаването на общоприетите подходи и практики, библиотеки и рамки, това е, което днес е знак за умението на програмиста.

В същото време, на красотата и магията на програмиране за мнозина (Сигурен съм, че не си сам в този) са напълно разкрити за решаване на сложни алгоритмични проблеми, толкова рядко срещани в ежедневната практика. И тъй като "в планината няма да дойде при Мохамед", че Мохамед е изобретил един пъзел от себе си!

Като подгряващи задачи за мозък, предлагам да се опита да научи компютър, за да се съберат пъзела известен "Петнадесет".

Петнадесет - популярната пъзел игра изобретен през 1878 г. от Ной Чапман. Това е колекция от идентични квадратни плочки с прикачени към номера, поставени в квадратна кутия. Дължината на полето четири пъти дължината на страничните пръстите за набор от 15 елементи (и три пъти за набор от 8 елементи), съответно, в заготовката за кутия остава един квадратен област. Целта на играта - движи пръстите на кутията, за да се постигне поръчване им по брой, за предпочитане прави по-малко движение, колкото е възможно.
Ключът към решаването на проблема ще стане известен алгоритъм за намиране на първото най-добро напасване на графика A *. За да се опрости представянето на проблема, аз ще разгледа пъзел с размери поле от 3 х 3.

Целият процес на намиране на решение на "маркер" може да се разглежда като проблем на полето за търсене. Върховете на тази графика ще озадачат поле състояние в резултат на изместване на кокалчетата на ръката:

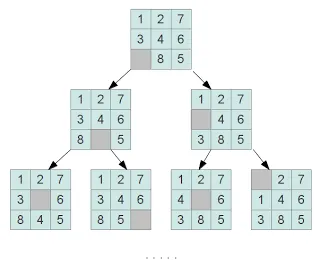
Търсене решения могат да бъдат сведени до намирането на статута терминал на игрална дъска (обикновено като терминал, избран подреждане на плочки подредени във възходящ ред от ляво на дясно, горе до долу).

За да се реши проблема с намирането на терминал в горната част на графиката, можете да използвате най-изчерпателни алгоритмите за търсене (дълбочина търсене или ширина), но броят на възможните решения (възможни пермутации) е вероятно да бъде достатъчно голям, за резултата от изчерпателно търсене няма да види до пенсионирането.

A * алгоритъм може значително да се намали броят на държавите, за да превъртате, чрез прилагане на някои допълнителни информационни евристични методи. Като такава информация се предлага да се вземе на прогнозния брой пермутации, необходими за получаване на терминал състояние.

За да се разбере как точно A * ви позволява да търсите в графиката, аз препоръчваме да прочетете статия A * алгоритъм за начинаещи. Материалите в този алгоритъм е писано толкова много, че нямам желание да се спра на подробностите, изложени по прилагането му, но въпреки това, за по-нататъшно разбиране на това какво се случва разбиране на A * алгоритъм е необходимо. Така че в кратко, аз все още ще обясни последователността от действия, предприети от алгоритъма за търсене на терминал състояние от примера на избрания решения пъзела.

A * алгоритъм предполага съществуването на два списъка с върхове: отворени и затворени. В първите върхове все още не са доказани алгоритъм, а вторият тези върхове, които вече са изпълнени в търсенето на решения.

На всяка стъпка от списъка с отворени върхове избран връх с най-ниско тегло. Тегло (F) на всеки връх се изчислява като сумата от разстоянията от първоначалното върха на ток (G) и евристичен предположение, че разстоянието от текущия възел към терминал (Н). F и G = I + Н аз. където аз - текущия връх (състоянието на дъската).

За "pyatnashek" можете да правите предположението, че за да се постигне в горната част на терминала, трябва да се извърши движение е не по-малко от броя на плочки, които не са на местата си, а разстоянието от първоначалното върха на тока се преброят на пермутации направени:

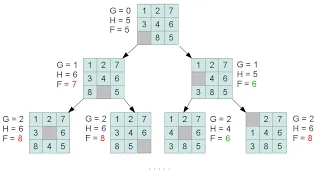
Освен това, за избрани върхове са генерирани деца възли (състояния, които могат да бъдат получени чрез преместване на плочки в празна клетка). Всеки възел има линк към родителя, т.е. "Помни" от коя държава идва.

Последователността на действията се повтаря до списъка с отворени върхове е най-малко по един връх или докато изпълнението на алгоритъма не отговаря на горната част на терминала.

разтвор Java.

A * се използва алгоритъм за решаване на голям брой задачи. Аз не искам да се ограничи неговото решение изпълнение само "pyatnashek". Ето защо, аз предлагам да се абстрахират от проблема да бъде решен с помощта на интерфейси, абстрактни класове и наследяване.

На първо място, проблемът да бъде решен чрез алгоритъма A *, различно определение на върха (или щати). Представяме абстрактен клас, който капсулира като цяло, за всеки два върха, поведение:

Освен това различните правила проблем на поколение от деца възли, алгоритъм за изчисляване на разстоянието от първоначалното връх и евристичен приблизителното разстояние до краен връх. Ние избираме тези функции в интерфейса:

Въз основа на тези абстракции, е възможно да се приложи алгоритъм A * е, както следва:

Това решение е малко по-малко от оптималното. Сигурно сте забелязали, че информацията в списъка на затворените върхове съкратените: ние никога няма да знаем детайлите на върховете на списъка, но само факта на принадлежност към върха му. За това не е достатъчно, за да се запази най-добре, както и стойностите на хеш функции.

Сега, по отношение на прилагането на пряко pyatnashek. Аз няма да се възпроизведе тук всички изходния код, можете да го видите в хранилището на bitbucket. Аз се съсредоточи само върху интересните, по мое мнение, нещата.

На първо място, удобно да представлява едномерен масив самото игрално поле, това ще се избегнат ненужни вложени цикъла, и като цяло е по-лесно решение да направи. връх разкриване алгоритъм (получаването му потомци), в такъв случай, получен е много проста. Първоначално, клетката е празна индекс се изчислява индекса на костите, който ще бъде преместен в празна клетка. Указателят се изчислява като сбор от индекса на празните клетки, а индексът на един от съседите си. съседни клетки елементарни кодове: за лявата съсед е -1, един за полето съсед, съсед горе - (размер поле), съсед дъно + (размер поле) на:

На второ място, за генериране на първоначалното състояние, първото нещо, което идва на ум е обикновено - е случайно подреждане на клетки върху игралното поле. Но този подход има голям недостатък. Ако вече сте погледна към уикито. знаете ли, че точно половината от всички възможни изходни позиции pyatnashek невъзможно да се доведе до събира ума. Това означава, че с този подход, рискувате да генерира такъв първоначален състояние, решение за което не съществува изобщо, или търсене на решение се отлага за непристойно за дълго време. За да не се развали му впечатление на извършената работа, можете да отидете на друг начин: това е възможно да се извърши N случайни пермутации правилни кокалчетата на ръката, като се започне от терминал състояние. Този подход гарантира за предоставяне на първоначалното състояние, има решение и го оставете да се коригира от сложността на търсенето:

UPD: На спешно искане на анонимен читател, ще опиша два привидно очевиден начин за генериране на първоначалното състояние.

Според формулата, посочена в Wikipedia, можете да проверите на първоначалното състояние на възможността да го доведе до краен среден:

Ние можем да покажем, че точно половината от всички възможни 1 307 674 368 000 първоначални позиции pyatnashek невъзможно да се доведе до събира ума (= 15!): Нека кутията с броя на създадени (ако броим от ляво на дясно и отгоре надолу) квадратчета с номера по-малки. Предполагаме, че е това, ако след кокалчетата с тия номера не по-малко от номера. Ние също така разглежда броя - броят на редица празни клетки (преброяване от 1). Ако сумата

е странно, а след това решите пъзела, не съществува.
И ако няма решение, регенерира първоначалното състояние. Позовавайки се на случая ще да не ми хареса, но и да избере една или друга ви подход. Във всеки случай, важно решение, а не първоначалното състояние :)

Процедура за проверка на първоначалното състояние:

Тестване на разтвора в действие: FifteenPuzzle.jar.

$ Java -jar FifteenPuzzle.jar -h

На мотивите на лекции по "Интелигентни системи".

Изразявам своята лична благодарност към Kopylovu Andreyu Valerevichu, за интересна презентация на курса.

Опитайте с друг критерий за определяне на теглото на върха. Не е броят на плочки, които не са на местата си, а общият път, който трябва да премине всеки джолан на мястото си. (За първи ъгъл от вашия пример, H = 10) Уредих конкурса и неговата си алгоритми, разликата в броя на възлите, които трябва да бъдат обработени достига поръчката. Петнадесет 4x4, тридесет смесващи пасажи (да, аз случайно прокара ходове):
ми алгоритъм
Отваряне на списък - 1668
Затворен списък - 1753
вашия алгоритъм
Отваряне на списък - 22317
Затворен Списък - 22452

"Основната му недостатък -. Това не винаги се намери най-краткия решение, въпреки че обикновено това е доста близо до него."

По принцип важи и за научни изследвания, не означава, че резултатът ще бъде, както се очаква. С A * и е най-краткият път _ischu_. Не е първия достъпен, а именно най-краткия. Фактът, че резултатът може да бъде различен от моите очаквания, техните, очаквания, не отрича :)

Опитайте вместо G вложка петите. Аз съм в затворената и отворената списъците, се оказва,
някъде, на 150 - 300 записи, средно. Ако следващото състояние е отворен или затворен списък, просто го игнорирате. И да, H изчислява като общото изминато разстояние от всяка кост на мястото си. Лодка кликне пъзел две секунди: D

. "Позовавайки се на случая ще да не ми хареса, но и да избере една или друга ви подход."

Искам да кажа, на случайността? Ако мястото на парчетата на терена не потвърждава, просто включете "надясно" (транспониране на матрицата) и да получите валиден състояние. Така че е съвсем нормално подход.