анализ функции например да парцел скица

Пример функция изследвания за парцел скица.

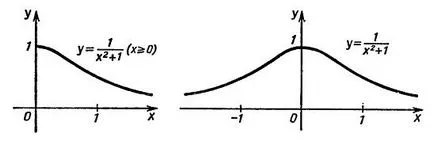
Ние се изследва функцията F (X) = 1 / (х 2 1) и в зависимост от резултатите направи скица график.

Първо, ние намерите функция достояние. Тъй като знаменател не изчезват в никакъв х, функцията се определя на цялата реална ос - х може да приеме всяка стойност. Имайте предвид, че функцията F (х) е още, тъй като е (Х) = 1 / ((- х) 2 + 1) = 1 / (2 х 1) = F (х). Тъй като функцията е дори, достатъчно е да се проучи и да се изгради eskih график само за положителни х, а след това се отрази скица отношение на ординатната ос. Сега ние откриваме, графиката на точките на пресичане с координатните оси. графика пресича точката (0; е (0)) с оста на ординатата. За нашата функция е точката (0, 1), тъй като е (0) = 1. За точката на пресичане с оста х, е необходимо за решаване на уравнение е (х) = 0. Уравнение 1 / (х 2 1) = 0 все още няма реални корени, тогава графика F (х) не се пресичат оста на абсцисата. От това можем да заключим, че или цялата функция графиката се намира по хоризонталната ос (функцията навсякъде положително) или по-ниска като цяло (отрицателна функция навсякъде) ,. Очевидно е, че фракция 1 / (х 2 1) за всеки X се положителни стойности, тогава график функцията на нашия цяло разположен над абсцисата.

При изграждането на графиката на функцията е много полезно да се разполага с информация за интервалите на увеличаване и намаляване функция. Използването на определението за увеличаване и намаляване на функции. Това може да се определи, че е (х) се увеличава в интервала (-, 0], и намалява в интервала [0). По този начин, в точката х = 0 е променен на увеличаване намаляването на функция. F (0) = 1.

Също така имайте предвид, че ако неопределен увеличение аргумент знаменател е (х) се увеличава за неопределено време, като по този начин стойността на функцията намалява до нула (произволно близо до нула). Въз основа на паритетен функция може да се каже, че функцията се държи по същия начин, както и с неограничен спада в спора.

Въз основа на получената информация, да можем да се направи скица на графиката, тя е представена на фигурата по-долу.