Алгоритми за намиране на най-късото разстояние в графиката

Заглавие на работа: търсене алгоритми най-късите разстояния в графика

Специализация: информатика, кибернетика и програмиране

Описание: Wanted за посещение на всички върховете на графиката и да се върнете към началния връх минимизира разходите за пътуване и свеждане до минимум на времето. Първоначалната информация е графиката, чиито дъги са възложени положителни числа разходите за пътуване или времето, необходимо, за да преминете от един връх в друг. Като цяло, графиката е ориентирана и на всеки два върха свързват две от дъгата напред-назад. Да предположим, че искате да намерите на разстоянието от 1-во до върха на всички останали.

Размер на файла: 194.5 KB

изтеглен на работа: 18 души.

проекция: Търсене алгоритми най-късите разстояния в графика Страница 2 от 2

[2] Алгоритъмът за търсене кратки разстояния в колона

[2,1] Dijkstra алгоритъм на

[2,2] краткия път проблем

[2,3] проблем максималната пропускателна

[2.4] Линейният програмиране докато максимизиране дебита

[3] тестови въпроси

Графиките са широко използвани както в областта на математиката и нейните приложения. Те се използват в строителството на различни математически модели на преносните мрежи, пътни мрежи, линии на въздушното движение и така нататък.

Искам да посетя всички върховете на графиката и да се върнете към началния p've автобуса, свеждане до минимум на разходите за пътуване (или свеждане до минимум).

първоначалната информация # 150; Тази графика, която дъги са определени положителни числа # 150; разходите за пътуване или времето, необходимо, за да преминете от един връх в друг. По принцип един чай в графиката е ориентирана, както и на всеки два върха са свързани с две дъги # 150; напред-назад. В действителност, ако точка А се намира в планината, и точка Б # 150; в долината, а от перспективата вози от А до Б, очевидно, по-малко време на обратния път от В до А.

Много продукции икономическо съдържание са намалени до проблема с пътуващ търговец. Например:

• създаде най-печелившата регулатор обходен маршрут в магазина (контролер, защитата и ка, полицейски служител), който отговаря за правилното функциониране на даден набор от предмети (ка w ди от тези обекти се моделира връх на графиката);
• създаде най-благоприятен начин за части или hleboz хляба работа и водата за определен брой пекарни и други обекти за търговия на дребно (за паркиране в пекарната).

Нека разгледаме някои типични проблеми на вземане на решения, свързани с оптимизиране на графики.

Алгоритъм на Дейкстра

Тази графика алгоритми, изобретени от Е. Dijkstra. Тя намира най-късото разстояние от един от върховете на графиката, за да всички останали. Алгоритъмът работи само за графики без ръбове на отрицателно тегло. Алгоритъмът е широко използван в програмиране и технологии, например, използва протокол OSPF за отстраняване на кръгови пътища.

Да разгледаме пример на алгоритъм на графиката, показана на фиг. Да предположим, че искате да намерите на разстоянието от 1-во до върха на всички останали.

Кръговете означават линиите на върховете # 151; пътеки между тях (ръбовете на графиката). Кръгът се посочва броят на върховете на краищата, посочени от тяхната "цена" # 151; дължина на пътя. В непосредствена близост до всеки връх обозначава с червен знак # 151; дължината на най-късата пътека в връх на връх 1.

Първата стъпка. Помислете алгоритъм на Дейкстра стъпка за този пример. Минимална марка има връх 1. съседите му са връх 2, 3 и 6.

Първият от тях с един съсед връх 1 # 151; Vertex 2, тъй като дължината на пътя, за да е минимално. Дължината в нея през горния 1 е равна на най-късото разстояние до горния ръб 1 + дължина става от 1 до 2, т.е., 0 + 7 = 7. Това е по-малко от настоящите връх маркерите 2, така че нов етикет 2nd пиковете е 7.

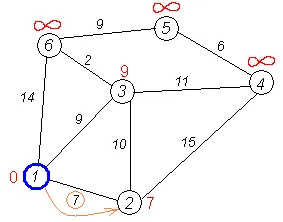
Ние правим една и съща операция с другите две съседи на първия връх # 151; 3-ти и 6-ти.

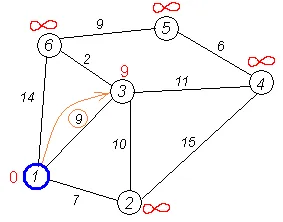
Всички съседи са на върха 1 проверени. Текущ минимално разстояние до най-богатия 1 е окончателно и не подлежи на обжалване (факта, че това е така, за първи път се оказа Дейкстра). Ние го изтриете от графиката. да се отбележи, че връх имаше.

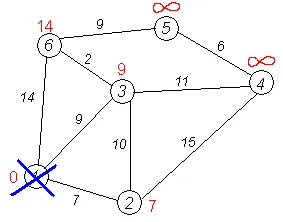
Втората стъпка. Етап на алгоритъма се повтаря. Отново откриваме "най-близкия" не са посетили върхове. Този връх 2 Маркирани 7.

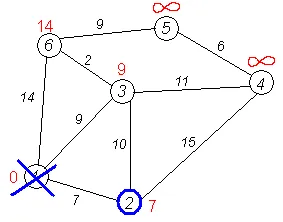
Отново, ние се опитваме да се намали съседните етикетите на избраните връх, опитвайки се да ги получите чрез 2-ри. Съседи връх 2 са 1, 3, 4.

Първата (в ред) съсед връх 2 # 151; връх 1. Но тя вече има, така че от 1-ви връх не правят нищо.

Следваща съсед връх 2 # 151; 3. Ако на върха, за да я държи на 2, след това дължината на такъв път ще е 7 + 10 = = 17. Но сегашната оценка е равна на третия връх 9<17, поэтому метка не меняется.

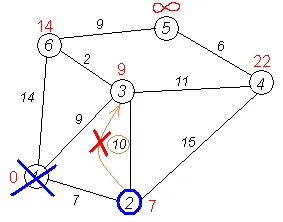
Друг съсед връх 2 # 151; 4. Ако пикът да влезе в него чрез 2-ри, тогава дължината на този път е най-късото разстояние = 2 + разстоянието между върховете 2 и 4 = 7 + 15 = 22. Тъй 22<. устанавливаем метку вершины 4 равной 22.

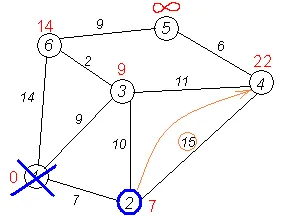
Третата стъпка. Повторете тази стъпка на алгоритъма от топ 3. След неговите "обработка", които получаваме следните резултати:

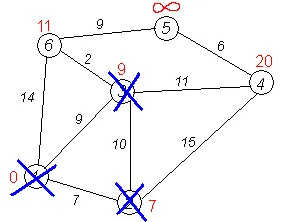
По-нататъшни стъпки. Повторете стъпка алгоритъм за останалите върховете (Това ще бъде от порядъка на 6, 4 и 5).

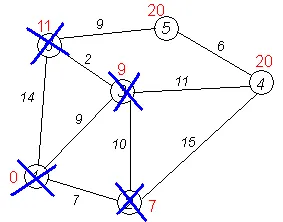
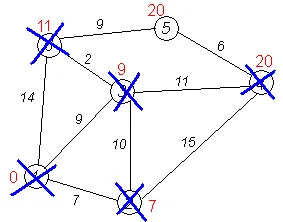
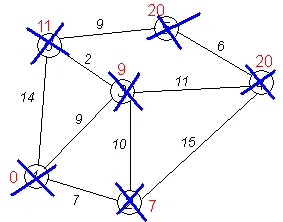
Завършване на алгоритъма. Алгоритъмът се прекратява, когато всички върхове са изтрити. Резултатът от работата му се вижда в последната фигура: най-краткия път от най-добрите 1 до 2 минути е от 7 до 3 минути # 151; 9 до 4-ти # 151; 20, 5-ия # 151; 20, 6-ия # 151; 11.

Най-къс път проблем

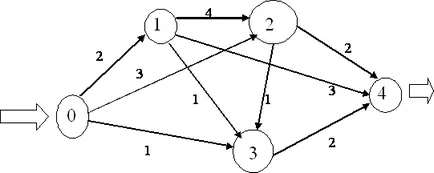
Като най-краткия път, за да получите от един връх в друг? От гледна точка на управлението на производството: как най-краткия път (и съответно с най-ниска консумация на гориво и време, най-евтино), за да се стигне от точка А до точка Б? За да се реши този проблем, всяка дъга от насочено графика трябва да се сравнява с броя на # 150; време на движение на дъгата от първоначалното връх до краен. Да разгледаме пример (Фигура 7).

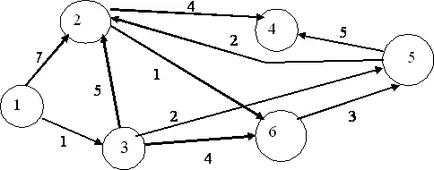
Фигура 7. Обстоятелства в основата на най-краткия път проблема.

Положението може да се опише не само насочена графика с тежести, приписана на дъги, но също таблица (Таблица 8).

Таблица 8. Обстоятелства в основата на най-краткия път проблема.

Предизвикателството: как да получите най-краткия път от връх 1 в топ 4?

Решение. Ние въведе нотация C (Т) # 150; дължина от най-краткия път от един връх на Т. връх Тъй като всеки път, който трябва да разгледа състои от дъги и арките на краен брой и всеки съдържа не повече от веднъж, кандидатите за краен брой най-краткия път, както и най-малко краен брой елементи винаги постигнати. Проблемът се състои в процес на разглеждане при изчисляването на C (4) и осигурява начини, по които се достигне този минимум.

За първоначални данни, показани на Фигура 7 и в Таблица 6, в горната част 3 е само една стрелка, само от върха и около 1. Тази стрелка е неговата дължина, която е равна на 1. Следователно, C (3) = 1. Освен това е очевидно, че G (1) = 0. Горният 4 могат да бъдат достъпни или от горната 2. късата пътека равно на 4 или 5 от горната след преминаване път равно на 5. Следователно връзката C (4) = мин.

По този начин, преструктуриран задача # 150; определяне на С (4) се редуцира до определяне на С (2) и C (5). Горният 5 могат да бъдат достъпни от горната 3. късата пътека равно на 2, или от връх 6. късата пътека равно на 3. Следователно връзката C (5) = мин. Знаем, че C (3) = 1. Следователно, C (5) = мин. Тъй като е очевидно, че C (6) # 150; положително число, последната връзка следва, че С (5 = 3. В горния 2 може да бъде постигнато или от връх 1, като път, равен на или от връх 7. 3. късата пътека равно на 5. 5. или от върха след преминаване пътека равно на 2. Следователно връзката C (2) = мин. знаем, че с (1) = 0, с (3 = 1, C (5) = 3. Следователно, с (2) = мин = 5.

По този начин, дължината на най-краткия път е 8. От тази връзка е ясно, че в топ 4, за да мине през най-горния 5.връщане за изчисляване на С (5), виждаме, че връх 5 да мине през най-горния 3. В топ 3 може да получи само един от върха.

По този начин, най-краткия път е както следва: 1 → 3 → 5 → 4.

Краткият проблем път за специфични входни данни (Фигура 7 и Таблица 6) е напълно решен.

проблеми за оптимизация на графики, които възникват при подготовката на управленски решения в управлението на производството, са много разнообразни. Помислете например за още един проблем, свързан с транспорт.

Максимална проблем поток

Кой маршрут да изпрати най-големият брой на товари от началната точка до крайната дестинация, ако пътищата трафик между точките, които е ограничен?

За да се реши този проблем, всяка дъга на насочен граф, съответната транспортна система трябва да бъде съпоставена с броя - капацитетът на дъгата. Да разгледаме пример (Фигура 8).

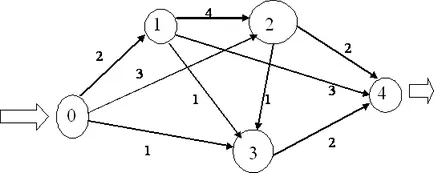
Фигура 8. Предистория на максимална проблема на потока

Първоначалните данни на транспортната система, например, в растение, показани на Фигура 8, може също така да бъдат определени таблица (Таблица 9).

Таблица 9. Предистория на максимална проблема на потока

Решението за максимална проблема на потока може да бъде получена от следните съображения.

Очевидно е, че максималната транспортния капацитет на системата е по-малко от 6, защото не повече от 6 единици на стоки може да бъде изпратен от началната точка 0, а именно единици 2, параграф 1, блок 3, параграф 2, и една единица в параграф 3.

Освен това е необходимо да се гарантира, че всички 6 излезе от 0 единици товар достига дестинация 4. Очевидно е, че 2 единица товар, който влезе в параграф 1, могат да бъдат директно изпратени до стъпка 4. Дойде в параграф 2 натоварвания трябва да споделят: 2 единици веднага да изпрати материала 4 и 1 единица # 150; 3 в междинна точка (поради ограничената производителност част капацитет между точки 2 и 4). В параграф 3, доставени тези стоки: 1 единица от 0 и 1 единица от т 3. Те са посочени в параграф 4.

По този начин, максималният капацитет на разглеждания транспортна система # 150; 6 единици багаж. Тя не използват вътрешни части (клонове) между точки 1 и 2, и между точки 1 и 3. dogruzhena клон точки между 1 и 4 # 150; Той се съсредоточи върху два товарни единици с капацитет от 3 единици.

Разтворът може да бъде представена като таблица (Таблица 10)

Таблица 10. Решението за максимална проблема на потока

Задачата на линейното програмиране като същевременно увеличава притока

Ние даваме на състав с максимална проблем поток от гледна точка на линейното програмиране. Нека X KM # 150; обем на трафик от точка към точка К М. Чрез Фиг.8 К = 0,1,2,3, М = 1,2,3,4, и транспортиране възможно само в точката с голям брой. Така че, всичко има 9 променливи X км. а именно, X 01 X 02 X 03 X 12 X 13 X 14 X 23 X 24 X 34. Проблемът на линейното програмиране, насочени към увеличаване на потока се определя от формулата: F → макс.

X 01 X + 02 + 03 X = F (0)
- X 01 X + 12 + 13 + X X 14 = 0 (1)
- X 02 - X 12 X + 23 + X 24 = 0 (2)
-X 03-X 13-X 23 X + 34 = 0 (3)
-X 14-X 24-X 34 = -F (4)
≤ 2 X 01

X KM ≥ 0. За M = 0, F ≥ 0, 1, 2, 3, 4.

тук F # 150; обективна функция, състояние (0) описва въвеждането на стоки в транспортната система. Състояние (1) # 150; (3) определя съотношението баланс за възли # 1 150 3 система. С други думи, за всяка една от вътрешните възли входящ поток на стоки е на отпадъчни води, товари и не се натрупват вътре в системата, а не на "Born" в него. Условия (4) # 150; Това състояние на "излизане" от системата на товари. Заедно с условието (0), представлява съотношението баланс на системата като цяло ( "въвеждане" е "изход"). Следващите девет неравенства поставят ограничения върху капацитета на отделните "клонове" на транспортната система. След това задайте без негативност на обема на трафика и целевата функция.

Ясно е, че последното неравенство следва от формата на обективната функция (връзка (0) или (4)) и обема на не-неотрицателност движение. Все пак, това неравенство има някаква обща информация # 150; чрез системата може да се пропусне или положителна стойност на товара, или нула (например, ако в системата има движение в кръг), но не и отрицателен (не от икономическа гледна точка, но формално математически модел не "знае" за това).

1. Определяне на алгоритъма за търсене на графики.
2. Принципът на работа на Алгоритъм на Дейкстра.
3. Да формулира проблема за най-краткия път. Обхват.
4. Формулиране на максимална проблем на потока. Обхват.
5. Формулиране на линейното програмиране проблем като същевременно увеличава потока. Обхват.

Tsentralnі ponyattya doslіdzhennya prognozuvannya главно parametrіv dіyalnostі organіzatsії. Suchasnі naukovі pіdhodi да rozumіnnya prognozuvannya главно Parametrіv dіyalnostі organіzatsії PROGNOZUVANNYA главно PARAMETRІV DІYALNOSTІ ORGANІZATSІЇ В SISTEMІ УПРАВЛЕНИЕ Suchasnyj PІDPRIЄMSTVA. Prognozuvannya в sistemі pіdpriєmstva управление strategіchnogo.

Романенко Kursova робот Ekonomichna efektivnіst virobnitstva rіpaku аз Пътища Ahead її pіdvischennya Студентски vіddіlennya Ekonomіka pіdpriєmstva Naukovі Основи pіdvischennya ekonomіchnoї efektivnostі virobnitstva rіpaku. Pokazniki ekonomіchnoї efektivnostі virobnitstva rіpaku тази техника їh viznachennya. Rіven virobnitstva rіpaku че Yogo Ekonomichna efektivnіst.