Трансформация в низ

Задачата на конвертиране на число в низ трябва винаги, когато искате да покажете цифровите резултати от програмата. Процесорите ще работят на двоични данни, от човека, както Дайте знак след десетичната запетая. Всъщност проблемът е да се превърне база броя. Какво да се прави, има начини? Целта на тази статия е да опише и сравни максималния брой начини за преобразуване на число в низ. Проблемът, разбира се, като се има предвид от гледна точка на изпълнението на микроконтролери, от размера и скоростта са важни. За простота, ние смятаме, само без подписани на 32-битови и 16-битови числа (не много по-трудно със знака).

1. sprintf

Първото нещо, което идва на ум е функция sprintf в стандартна библиотека. Използвайте го, просто:

Тогава в буфер масив се изисква в нашата линия.
Но проблемът е, че е sprintf форматиран функцията за изход, който е много неща може и дърпа много други функции на стандартната библиотека. Размерът на машинен код, когато се използва, нараства значително. Например, дори минималната версия на sprintf AVR-библшотеката (това е, което е част от WINAVR / AVR Toolchain) добавя малко по-малко от 2 килобайта.

2. utoa, ultoa

Съставът на библиотеки, предоставени с компилатори често включва трансформиране функция на низ itoa, ltoa, utoa, ultoa. Като цяло, тези характеристики не са стандартни, краката са често на разположение, както и, за разлика от sprintf, не правите нищо допълнително.

3. Извличане на номера чрез разделяне на 10.

Готов стандарт и не много модни тенденции. Сега е време да преосмисли своите велосипеди. Първият най-лесния начин е, разбира се, разделена на 10, а останалата част в цикъла на изчисление.

Останалата част от разделението ни дава десетични цифри в обратен ред, като се започне с най-малките, така че пиша от буфера, считано от края, така че не се разгърне в резултат на низ.
Всичко изглежда просто красива, нищо повече, но има едно нещо. Всъщност разделение, а дори и изчисляването на баланса. Ако процесорът не е разделението на хардуер, това е много бавен.

4. Премахване на номерата дивизия 10 чрез функция Разделение

Може да се опитате да използвате стандартната функция DIV, който веднага се връща на частното и остатъка?

Но разделението все още остава. Предимствата на този и предишния метод е фактът, че те може да конвертира броя в низ по някаква причина (ако Yoh леко променя), а не непременно 10.

5. Разделя се на 10 смени и допълнение.

Ако целевата процесора не разполага с хардуерна поддръжка за 32-битово разделение, предишните два метода са доста бавни. Division 10 може да бъде заменен с поредица от смени и допълнения. Вдъхновен от книгата "алгоритмичните трикове за програмисти" (това е «наслада хакери» една и съща), извадете функцията за разделяне 10 използване на смени и допълнения, замяна на съществуващите там, умножена по 10 (това е прекалено "скъпо" за AVR, най-малко), както е измести и допълнение. Ние го променят така, че да се връща и частното и остатъка:

Тя изглежда ужасно и не е ясно, но това всъщност е лесно. Първо, ние умножи първоначалния брой от 0,8 или 0,1100 1100 1100 1100 1100 1100 1100 1100 в двоичен представителство. Това е много удобно, че фракцията периодична и успя да направи всичките пет смени и четири допълнения. Следваща разделят какво се случи с 8, измества надясно с 3 разряд. Оказва се, първоначалния брой делено на 10, до блок поради закръгляване грешки. След като се намери полученият остатък, чрез умножаване с коефициент от 10, и това изваждане от първоначалния брой. Ако остатъкът е по-голямо от 9, а след това и лично се адаптира.
Функцията използва "бърза" деление не се различава на външен вид от своите предшественици.

6. Извадете 10 градуса.

Друг популярен метод за конвертиране на число в низ, се изважда от оригиналния сериен номер от 10 градуса, като се започне от най-много. Вие ще трябва една маса с тези градуси 10:

40 байта. И самата функция:

Works е проста, толкова дълго, колкото текущия брой е по-голям от 10 градуса го изваждат от тях броят на 10 градуса и да се разгледа колко време се изважда. След това отидете в по-ниска степен на 10. Така че, докато не стигнем до 1. Данните са получени директно в желания ред, само трябва да се премахне нули.

Методи BCD числа.

Следните три методи се основават на операции с опаковани двоично кодиран знак - двукомпонентни кодирани десетични знака (BCD). В това представяне, всеки хапане (4 бита) съхранява десетичната цифра. По този начин в променливата на 32-битова да съхранявате 8 десетични цифри. Двоичното представяне на променлива с 2-битов е 10 десетични цифри. Следователно, тези методи дават резултати подрязани за номера по-голям брой 99999999. BCD е много лесно преобразувани в поредица:

Всъщност от дейността на BCD, трябва да добавим и се умножава по 2, което е успешно заменя със събиране броя със себе си. Ето защо, трябва само добавянето на:

Тя изглежда ужасно и не е ясно - отново някакъв сложен растерни Mojo. В действителност, за добавяне на два BCD просто ги добавят като конвенционални двоични числа - линия + = б. И тогава за всеки заяждам, чиято стойност е повече от 9 нужда да се добавят броят корекция 6 с прехвърлянето на бита в най-значимия хапане. А на всичките хапане на която беше прехвърлянето на бита в най-значимия хапане, трябва да се прибави броят корекция 6. Всички останали линии функционират - това именно е корекция. Първите две линии, ние определят всички битове обобщават A + B + 0x66666666ul. който се променя стойността си поради преноса на LSB малко. В третия ред добавим нашите две числа. В четвъртия - изберете по-ниските трансфер бита за всеки четворка. В други - 6 добавим към тетради от които са прехвърлени бита. Ето как - без условно прехвърляне.

7. Добавяне на правомощията на две.

Първият метод е добре познато на всички от ученическите си уроци по компютърни науки, - добавяне на знака след десетичната представяния на правомощията на две, съответстващи на едно малко в преобразуваната номер:

7. Добавяне на правомощията на две с масата.

В предишния метод използва два сумиране BCD числа. Един от тях може да се елиминира, като степен на две от масата:

Таблица elmentov съдържа 30 - 120 байта.

8. метод на Хорнер

При този метод, на всеки етап от удвояване на натрупаната знак резултат, ако MSB на бинарен номер едно, след това се добавя към единица резултат, където бинарен номер се умножава по 2 (смяна на малко вляво).

Тук освен операцията два BCD, но един от тях с добавка на 1 и от него не може да се освободи.

В този случай, първата bcd_add аргумент не може да бъде валидна BCD, където по-млад се заяждам с цифра по-голяма от 9. Но нашият bcd_add обикновено се дъвче даде правилния резултат. Но ако добавите тази допълнителна единица на втория аргумент, резултатът вече не е вярна.
Броят на повторения в цикъла на този метод винаги ще бъде равен на броя на битовете, за разлика от предишните, при които цикълът ще приключи веднага след като няма да има тези на отделни битове.

9. вземете номерата се умножи по 10.

Сега всъщност частта, за която всичко започна - сравнение на скоростта. Първата платформа ще бъде тествана с помощта на AVR GCC компилатор.
За методите на различни видове време ще зависи от различни фактори, като например методи, основани на разделение от 10 път ще зависи до голяма степен от броя на десетични цифри от абсолютната стойност е броят и много малко от самите тези номера. Изваждане на 10 градуса в цикъл ще бъде по-бързо, отколкото да работят по-малка сума от десетични цифри грим числата. Това е 1000000 обработва много по-бързо, отколкото 999999. Методът се базира на номерата на двоично-десетичен ще работи по-бързо, ако първоначалният брой малки отделни битове - най-бързият чрез мощности на две. последния метод на работното време, ще зависи само от абсолютната стойност на преобразуваната брой, но по-малко в сравнение с методите за разделяне на 10. Така че в този набор тестове трябва да бъдат малки Чила, големи номера, мощност от две до десет градуса, където много деветки.
Всички видове тестове за AVR е удобно, извършвани на Simulavr симулатор - не е нужно никой желязо, както и множество pereproshivok.
За измерване на времето за изпълнение на нашите функции, които използваме таймер 16-битово тиктака в основната честота. Console изход чрез отстраняване на грешки пристанище емулатор. код за оптимизиране на максималната скорост.
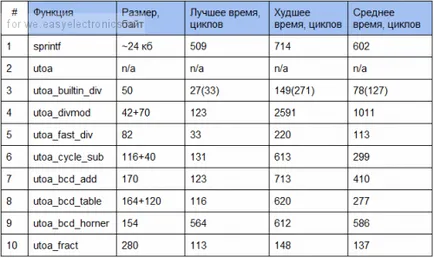
Ето какво се случи в резултат на 32-битови числа:

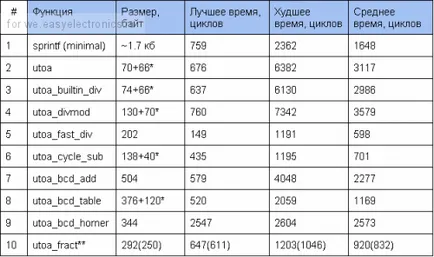
* След зависимостта на размера плюс - функция маса или разделяне
** в скоби са резултатите за варианта с модула на вградени.

Лидерът в този показател с не голям марж метод за бързо делящите 10 смяна и допълнение. За да го получите, близки изваждане градуса 10. След умножение по метода 10. Методите с честен дивизия (включително utoa), както се очаква, много бавно, особено такава, която използва ldiv функция. но също така и най-компактните. Изпълнението на метода на Horner е почти независим от преустроена номер. sprintf работи сравнително бързо, в сравнение с utoa. И не е чудно - тя се използва в метод, подобен на utoa_fast_div, но натоварването при анализирането на низ за форматиране и бавно изхода към буфер чрез fputc се проявяват.

UPDATE.
Резултати за 16-битови числа:

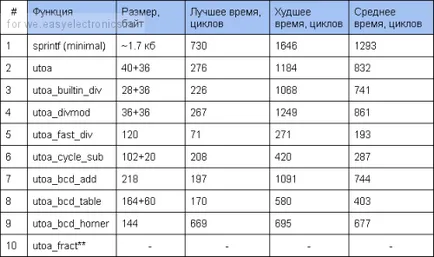
Тук отново с забележимо предимство на водещи подразделение на бързото смени / сгънати. Лошият резултат сега sprintf, защото вътре тя все още използва номер 32-битова.

UPDATE # 2. Резултати за MSP430.

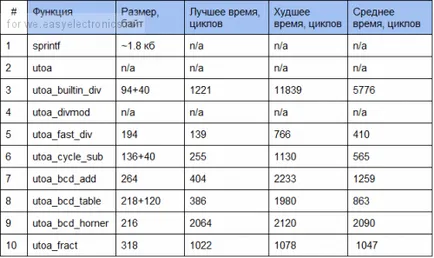
Резултати за 16-битови числа:

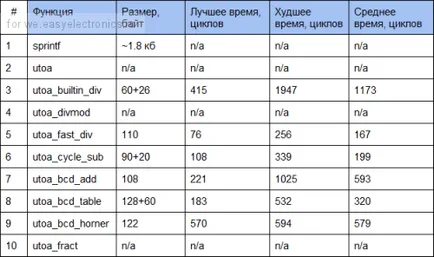
Тъй като в допълнение към MSP430 Launcpad-и с камък MSP430G2231 друга MSP430 Аз не трябваше да го тестваме. Всички функции на Разбира се, че не се вписва, на заливаеми и тествани един по един, като се използва скрипт.
Както можете да видите по-справедливо разпределение тук е почти два пъти по-бавно от AVR.
UPDETE # 3

Резултати за STM32.

обсъждане на резултатите

Аутсайдер навсякъде функция на използване на функцията библиотека разделение Разделение. Въпреки факта, че той се връща в един разговор, а остатъкът и частното, дори STM32 разделението хардуер, тя се изпълнява в областта на софтуера и работи много бавно. Очевидно е, че не трябва да се използва този метод. Въпреки това, функцията използва вграден в дивизия оператор utoa_builtin_div. преплитане в края на AVR и MSP430, на STM32 - води. Не е изненадващо, тъй като в Cortex M3 има разделение хардуер, мнозина казват, и не са съвсем наред - разделянето на нещо там, но това не е толкова бързо (в скоби за utoa_builtin_div определено време, ако компилатора да генерира справедливо разпределение). Фактът, че ССЗ трудно, когато се раздели на постоянното използване на хитър трик - замества разделение чрез умножаване с постоянен, така че горните 32 бита в 64-битов продукт да съдържат оригиналния дивидент делено на 10.

Този код е еквивалентно на приблизително следното:
uint32_t ТМР = стойност;

Този метод също е описан в книгата "алгоритмичните трикове за програмисти." Въпреки това, AVR и MSP430 този номер няма да работи - има умножение на 32 * 32 => 64 творби неприлично дълго, дълго справедливо разпределение.
Друг utoa_builtin_div винаги има минимален размер.
Винаги добро и често по-добър резултат дава деление с 10 смени и допълнение utoa_fast_div. Това е почти безспорен лидер в скоростта и често е доста скромни размери. Този метод винаги е добър избор.
Обичан от много градуса изважда десет utoa_cycle_sub по размер с таблицата за една и съща sutoa_fast_div. но винаги дава малко скорост. Като цяло, също не е лош избор.
Методът се основава на двоични десетични числа не работят много бързо, не разполагат с най-малкия размер и на един и същ въпрос само 8-цифрен резултат (в моя изпълнение, можете да получите всички 10 числа, но ще бъде още по-бавно). По-добре е да не се използва за преобразуване на двоични числа в низове и за преобразуване на двоични числа в десетични двоичен опаковани, излитане за по-нататъшна работа.
Отделно е метод на размножаване с 10 utoa_fract. Той не изглежда много привлекателно в средното време, обаче, това е най-лошото време често е по-малко от най-лошите лидери от време. При този метод, разликата между най-добрите и най-лошото е относително малък - той е стабилен.

UPDATE.
Открих още един интересен и много бърз метод. Ето тук.

Описание на това как тя работи от линка по-горе на английски език. За съжаление, на правилните резултати, този метод се произвежда само 15-битови стойности, но много бързо:
за AVR-добрият момент - 133 цикъла, най-лошото - 167 средната - 146.

Очаквайте следващата.

Част 2: Фиксиран и плаваща запетая.

PS. Може би някой знае още какви някои методи за преобразуване на числа в низ?

Избрано по метод, основан на фракции или редове, аз не знам как да го кажа. Ако вие ще получите - Аз ще очертае материала (това е необходимо или не - Говори). Но предварителните резултати без съхраняване на дробна част по-лошо.
neiver. ще тества как да се опише, ако все още prisutsvuete на сайта?

5 изпитани метода за пореден път на цялата гама от uint32_t. Не са открити отклонения.
codepad.org/AZcD1P5Y

Хмм ... Оказва се, че за пръв път не ми е ясно на алгоритъма е: не се заяждам (niibly, 4-битова) копие, и всеки път, когато се удвоява броят на битовете, използвани за размера на натрупване. Хитър!

Грешката се заобиколят автоматичен резултат на корекция.
Добавянето на още една смяна в 32 и с помощта на 64-битови стойности също беше точни стойности. Тя изглежда като грешка при закръгляването се компенсира в получената сума не е съвсем ясно за мен начин, защото с отделни тетрадки (в този случай съвпада с периода на фракция (1100) кошчето за), грешката се натрупва.
Благодаря ви много за статията!

Нека обясня за какво съм написал, и тя се чувства паникьор. 52 (с разлагане) и се ограничава до 8 бита.
Както се оказва, последователността от действия е важно, това е, не можеш да nasdvigat, след което добавете резултатите от промените, е необходимо от натрупването на всяка смяна. Нещо като еквивалент трябва да се k.m.k.