Selfadjoint (Hermitian) оператори и техните свойства
Измерва директно (на "наблюдаваното") са реални физически стойности, т.е. всички собствени стойности -
1) ако физическа система (частиците) е в състояние, описано от своя собствена функция. когато се измерва получи съответния собствена стойност GN;
2), ако системата (частиците) е описан от произволна функция. когато се измерва наблюдава, т.е. действие на оператора. Ние се получи линейна комбинация от GN собствените стойности - някои средна стойност, която също е реална.
Представяме на концепцията за транспонирана оператора. която се определя от отношението
т.е. транспониране на същия ефект, като действа по левия функция като тази на оператора. Действайки прав.
оператори Самостоятелно долепени се определят от следното уравнение
където - конюгат оператор на оператора.
този оператор се нарича Hermitian или самостоятелно долепени оператор. Можем да кажем, че действието на оператора в дясно от него функцията съвпада с действието на комплекс конюгат оператор на функцията вляво:
По този начин, операторът на прилежаща - е комплекс конюгат транспонирана оператор от оператор
Помислете за диференциално оператора. Ние приемаме, че функциите на вълна са равни на нула в безкрайността. Изчисляваме оператора долепени на оператора чрез интегриране по части:
По този начин, операторът на прилежаща оператор. е
и поради това, операторът не yavlyaetsyaermitovym. Очевидно е, че
инерция оператор - самостоятелно долепени оператор.
Операторът координира и Hermitian оператор.
Да разгледаме уравнението и
Това уравнение означава, че собствените стойности на Hermitian оператор са реални.
Продуктът на две Hermitian оператори пътуване до работното място има Hermitian оператор
Да предположим, че имаме дискретен комплект собствени стойности и eigenfunctions на Hermitian оператор (и вярвам, че няма духовен упадък, т.е. всички вълнови функции са различни за различните собствени стойности):
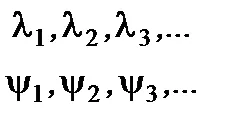
В математиката строго доказано, че наборът от eigenfunctions на Hermitian оператор представлява цялостна система от ортонормирани вълнови функции, т.е.
В действителност, за да докаже, ортогоналност разгледа две уравнения
Умножаваме първото уравнение в ляво. вторият от. и да се интегрират. Изваждайки второто уравнение от първото уравнение и като се има предвид, че (- Hermitian оператор). получаваме:
,
От това следва, че ако LN ¹ LM. след това. Пълнота на комплекта означава, че всяка функция може да се разшири в редица функции.
В случая, когато имаме дегенерация, вълновата функция се приема като линейна комбинация. където всички функции на вълните имат същите собствени стойности. Линейните комбинации могат да бъдат направени така, че новите функции на вълните са ортонормирани.
Разглеждане на разширяването на произволна функция последователно в системата на eigenfunctions на самостоятелно долепени линеен оператор
Коефициентите за разширяване могат да бъдат получени чрез умножаване на двете страни на експресия чрез интегриране и:
коефициент на квадрат | | Тя дава вероятността, че е описал състоянието. Настоящото състояние на примеси.
Ако имаме непрекъснат диапазон от стойности, а след това на вълновата функция, за да се разложи на интеграл
където коефициентите се определят
непрекъснатост спектър вълни са нормализирани към D - функция
Функцията е нула навсякъде освен в точка х = а. където тя става безкрайна: