Ролята на бързо молекули
Във всеки температура има редица молекули, които ускоряват и следователно кинетична енергия, значително по-висока от средната.
Известно е, че много химични реакции, като например изгаряне на конвенционални горива (дърва, въглища, и така нататък. D.), изхождайки само в определен, достатъчно висока температура. Енергията, необходима за стартиране на процеса на окисление на горивото, т.е.. Е. горене (наречена енергия активиране), е от порядъка на 10 -19 J .. И при 293 К (стайна температура), средната кинетичната енергия на топлинна движение на молекулите е приблизително 5 х 10 -21 J. Ето защо, не се случва за парене. Обаче, повишаване на температурата само два пъти (до 586 К) причинява възпаление. Средната енергия на молекулите увеличава в същото време също е фактор от 2, но броят на молекули, кинетичната енергия превишава 10 -19 J, увеличава 10 8 пъти. Това е следствие от разпределението на Максуел. Ето защо, при температура от 293 К, се чувстваш, четене на книга, удобни, и при 586 K книга започва да гори.
изпаряване на течността и се определя от бързо молекули отдясно на "опашка" на Maxwellian разпределение. Свързващата енергия на водни молекули при стайна температура, значително по-дълго KT. Въпреки това, изпаряване се дължи на малкия брой на бързо молекули, чиято кинетична енергия надвишава KT.
Максуел открили нов вид физически закон - статистическа и е установено, разпределението по молекулна скорости. Той ясно да се разбере значението на откритието си. Докладът на Максуел на Кеймбридж Философски общество заяви: "Смятам, че най-важното за развитието на нашите методи на мислене има молекулна теория, защото те са принудени да се прави разлика между двата метода на знание, което можем да наречем един динамичен и статистическа."
§ 4.7. Измерване на скоростта на молекулите на газа
Основният уравнението на молекулно кинетичната теория на газовете (4.4.9) се получава на базата на идеалния модел на газ. В този случай, няколко опростяващи допускания, реалната картина е направена. За да се провери годността за приемане на направените допускания, трябва да се провери експериментално получена от уравнението (4.4.9) на разследването. Една от основните последици от молекулно кинетичната теория основното уравнение е зависимостта на средното квадратично скоростта на термична движение на молекули (газ микроскопични характеристики) на температурата (макроскопични характеристики на състоянието на газ). Тази зависимост и може да бъде проверена експериментално.
Средната скорост на топлинната движение на молекули
От сравнението на (4.4.9) с термодинамична уравнение на състоянието на идеален газ е получен чрез експресия (4.5.5) за средната кинетичната енергия на транслационно движение на молекулите:
Следователно, средната квадратична скоростта на постъпателно движение е:
Корен квадратен от това количество се нарича квадратичен средна скорост:
Средноквадратичната скорост е малко по-различна от най-вероятната скорост даден чрез експресия (4.6.9). Тъй като Болцман константа, равна на константата на съотношение универсалната газова константа на Авогадро
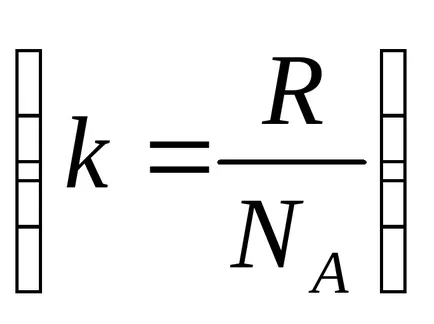
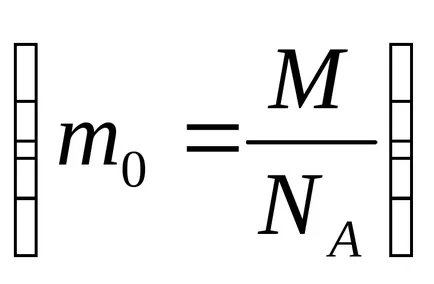
Изчислена чрез тази формула скорост

Както се вижда от таблица, скоростта на молекули са много големи - от порядъка на скорост артилерийски снаряди - и малко по-голяма от скоростта на звука в съответния газ. На първо място, като в резултат води до объркване сред физиците. В крайна сметка, ако скоростта на молекулите са толкова големи, как да се обясни, например, миризмата на парфюм, разлято в стаята, разпространява доста бавно; Трябва да отнеме няколко секунди да миришат разпространи в цялата стая. Но, за да обясни този факт е доста проста. газови молекули, въпреки малкия си размер, непрекъснато се сблъскват една с друга. Поради големия брой молекули ускори сблъсък на въздушните молекули в едно секунди при нормални атмосферни условия до няколко милиарди.
Средният свободен пътя на молекули е равна на 10 -4 -10 -5 cm. Следователно, траекторията на всяка молекула е много сложен полигон (фиг. 4.14). Голям молекула има скорост на правите участъци от наклонен. Преместването на една и съща молекула в определена посока е малък дори в средата на времето на няколко секунди. При преместване молекули от точка А до точка В пътя преминава е много по-голяма от разстоянието AB.

За да продължите с изтеглянето, което трябва да се съберат на снимка: