Решение на линейната система от уравнения с три неизвестни - Математика
Решете системата на линейни уравнения по два начина: чрез правило Крамър и от Гаус
1) решаване нехомогенни система линейни уравнения Ах = Б от Kramer
Определящо система D не е равна на нула. Ние считаме, помощни детерминанти D1. D2. D3. ако те не са равни на нула, а след това няма никакви решения, ако равен, а след това един безкраен брой на решения
3 Системата на линейни уравнения с три неизвестни, чиято детерминанта е различно от нула, е винаги постоянна и има уникален разтвор, изчислена както следва:
A: имам решение:
2) решаване нехомогенни система линейни уравнения метод Ах = В Гаус
Ние образуване на разширената матрица на системата
Да вземем първата линия на ръководството, и елемент A11 = 1 - за ръководството. С помощта на направляващи линии получи нули в първата колона.
Матрицата, съответстваща на набор от разтвори на системата на линейни уравнения
A: имам решение:
Като се има предвид координатите на върховете на триъгълника ABC
1) дължината на страната AB;
2) от страните AB и BC и техните ъглови коефициенти;
3) на вътрешната ъгълът в радиани до 0.01
4) AE средната уравнение;
5) уравнение и височина дължина CD;
6) уравнението на линия, минаваща през точка Е успоредна на страната AB и точка М на пресичане с CD височина;
7) уравнението на окръжност с център в точка Е, минаваща през върха B
Изграждане на даден триъгълник и всички линии в координатна система.
1) разстоянието между точка А (х1, Y1) и В (x2, y2) определя по формулата
използване на който ние намираме дължината на страната AB;
2) от страните AB и BC и техните ъглови коефициенти;
Уравнението на линията, минаваща през двете дадените точки А равнина (х1; Y1) и В (x2, y2) е с формата
Заместването в (2) на координатите на точките А и В, ние получаваме уравнението на страните AB:
Наклонът на линията AB Kav намери превръщане на полученото уравнение на формата на уравнение права линия с ъглов коефициент у = KX - б.
Ние, това е, когато
По същия начин, ние получаваме уравнение директно слънцето и да намерят своя наклон.
Заместването в (2) на координатите на точките В и С, се получават уравнение страна пр:
Ъглов коефициент на правата линия BC КВС намери превръщане на полученото уравнение за уравнение права линия означава на наклон у = KX - б.
3) на вътрешната ъгълът в радиани до 0.01
За да намерите нашия вътрешен ъгъл на триъгълника, които използваме формулата:
Имайте предвид, че реда на ъгловата разлика изчисляването на коефициентите в числителя на фракцията зависи от относителното положение на линии АВ и ВС.
Заместването по-рано изчислените стойности и КВС KAV в (3), намираме:
Сега, с помощта на електронни таблици инженерни калкулатори, получаваме Б "1.11 рад.
4) AE средната уравнение;
За съставянето на средната уравнението AE първо намерите координатите на точка Д, който се намира на среден сегмент пр.н.е.
Замествайки в уравнение (2) координатите на точките А и Е, които намираме средната уравнение:
5) уравнение и височина дължина CD;
За съставянето CD уравнения височина използват уравнение права линия, минаваща през дадена точка М (x0, y0) до предварително определена ъглова коефициент к, която има формата
и състоянието на перпендикулярност линии АВ и CD, което съотношение е експресиран Каб KCD = -1, където KCD = -1 / Каб = - 3/4
Заместването в (4), вместо на стойността к KSD = -3/4, и вместо x0. Resp y0 координатна точка C, ние получаваме компактдиска уравнение височина
За формулата за изчисление за намиране на височините на разстояние използват CD дължина г от дадена точка М (x0, y0) до предварително определена права линия с уравнение Ах + С + С = 0, което е от вида:
Заместването (5), вместо x0; Y0 координати на точка В, и вместо А, В, С коефициенти на линията AB, получаваме
6) уравнението на линия, минаваща през точка Е успоредна на страната AB и точка М на пресичане с CD височина;
Тъй като се изисква права линия EF е успоредна линия AB на това KEF = Каб = 4/3. Заместването в уравнение (4), вместо x0; y0 координатна точка E, но вместо на стойност к Кеф получи линейно уравнение EF ".
За да намерите координатите на точка М заедно решава уравнения линии EF и CD.
Така, M (5,48; 0,64).
7) уравнението на окръжност с център в точка Е, минаваща през върха B
Тъй кръга е центъра на точка Д (4.5, 2) и преминава през връх V (4, 3), радиус
каноничен уравнение окръжност с радиус R центриран в точка M0 на (x0, y0) се дава от
триъгълник АВС на височината на компактдиска, медианата на AE, директен EF. точка М и кръг изработена x0u координатна система на Фиг.1.

Създаване линия уравнение за всяка точка от които неговото разстояние до точка А (2; 5) е равно на разстоянието до линия у права = 1. Полученото конструкт крива в координатна система
Нека М (х, у) - текущата точка на желаната крива. Капка от точка М MB перпендикулярна на линията Y = 1 (Фигура 2). Тогава В (х 1). Тъй MA = MB. на

Получената уравнение определя парабола с връх в точка С на (5; 1.5) и клонове, насочени нагоре (вижте Фигура 2).
Намерете в определените граници:
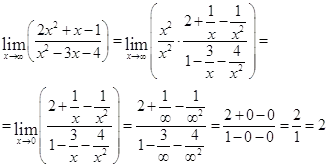
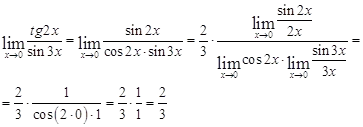
Намери производно ди / DX, като се използват правилата и диференциация формули

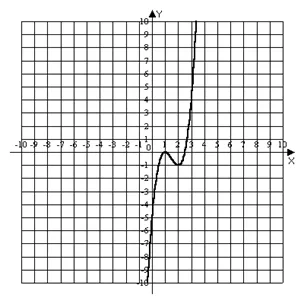
За да се изследва функцията е посочено методи за диференциално смятане да изготвят своите графики.
1) домен на тази функция са всички реални стойности на аргумент X, т.е. D (у) =, и това означава, че функцията е непрекъсната по цялата реално линия и графика все още няма вертикални асимптоти.
2) проучване на функцията на екстремум и монотонност интервали. За тази цел, ние откриваме, неговите производни и се равняват на нула:
Решаването на полученото квадратно уравнение можем да заключим, че функцията има две критични точки от първия вид x1 = 1, x2 = 2.
Ние разделят домен на тези точки на части и да ги променя подпише функцията производно разкрие монотонност интервали и като екстремумите:
стойност х В = 1.5 е абсцисата на инфлексната точка на графиката на функцията, а ординатата на тази точка:
4) Да се определи наличието на дадена функция графика асимптоти. За да се определи асимптота параметър уравнение у = KX - б използват формулите
По този начин, графиката на дадена функция не е склонен асимптоти.
5) се конструира графиката на
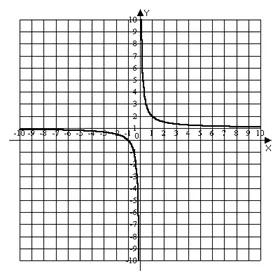
1) домен на тази функция са стойностите на аргумент х
2) Проучване на класификацията на приемственост и прекъсване точки
Желаният функция е непрекъсната навсякъде освен в точката х = 0. изчисли своите едностранни ограничения в този момент:
Така че точката х = 0 - точката на прекъсване от втори вид, и линията х = 0 - вертикална асимптота.
3) проучване на функцията на екстремум и монотонност интервали. За тази цел, ние откриваме, неговите производни и се равняват на нула:
Следователно, функцията все още няма критични точки от първия вид.
Тъй като Y ' <0 для всех х, то функция убывает во всей области определения
4) определяне на инфлексна точка на графиката на интервали и изпъкналост и вдлъбнатината. За да намерите втората производна на дадената функция и да го настроите равна на нула:
Така че функцията все още няма инфлексни точки. Ние разделят областта на точката х = 1, всеки от които се установи знака на втората производна:
5) Да се определи наличието на дадена функция графика асимптоти. За да се определи асимптота параметър уравнение у = KX + б ние използваме формулите
По този начин, графиката на дадена функция има наклон асимптота
6) се конструира графиката на функцията
Информация за "решаване на линейната система от уравнения с три неизвестни"
Категория: Математика
Брой знаци с интервалите: 7857
Брой на маси: 3
Брой на изображения: 7