Просто средно аритметично
Широко разпространени статистически данни са средни стойности.
Средната стойност - обобщение мярка, която намери израз експлоатация на общите условия, законите на развитие на явлението, които се проучват.
Статистически средна се изчисляват въз основа на данни от мас правилно статистически организирано наблюдение (общо и за вземане на проби). Въпреки това, средната статистическа е типична цел и, ако се изчислява на данните на теглото, за качествено хомогенна популация (масово явления). Например, ако се изчисли средната заплата в акционерните дружества и държавните предприятия, а резултатът е удължен до целия набор, тогава средната стойност е фиктивен, както е изчислено от нееднородно население, а това средният няма смисъл.
С среда възниква като изглаждане на различията в размера на функция, които се случват по различни причини, отделните звена на наблюдение.
Така например, средната мощност на отделен продавач зависи от много фактори: квалификация, опит, възраст, под формата на социални грижи, здравеопазване и т.н. Средната мощност отразява общата характеристика на цялото население.
Средната стойност се измерва в същите единици, както самият знак.
Всяка средна стойност характеризира целевата популация на която и да е функция. За да получите пълна и цялостна картина на целевата група, към редица съществени функции, трябва да имат система за средни стойности, които могат да опишат явлението от различни ъгли.
Има различни видове средни:
Средната стойност на всички тези видове, от своя страна, са разделени на прост (непретеглена) и претеглени.
Помислете за вида на средни стойности, които се използват в статистиката.
Средноаритметичната стойност на прост (не претеглените) е сумата от отделните характерни стойности, разделен на броя на тези стойности.
Някои характерни стойности се наричат варианти и означени с XI (
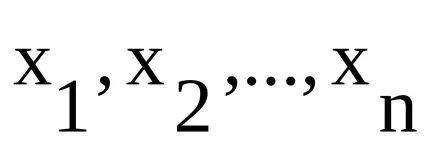

Пример 1. Таблица 1
Продукция данни работници на смяна A
В този пример, различна функция - освобождаване на продуктите на смяна.
Числените стойности на характеристиката (16, 17, и така нататък. Г.) се наричат варианти. Ние определяме средната мощност на продукти от тази група работници:
Просто средно аритметично се използва в случаите, когато има определен характерен стойност, т.е. данните не са групирани. Ако данните са под формата на серия или групи за разпространение, средната стойност се изчислява по различен начин.
Претеглена средна аритметична
Средноаритметичната стойност е претеглена сума на продуктите на всеки отделен характерна стойност (вариант) за правилното честота, разделен на сумата от всички честоти.
Брой идентични характерните стойности в редиците на разпределението се нарича честотата или тежестта и е означен с Fi.
В съответствие с това, претеглена аритметична стойност е:
Формулата показва, че средната стойност зависи не само от характерните стойности, но също така и на техните честоти, т.е. състава на съвкупността от неговата структура.
Пример 2. ТАБЛИЦА 2
Данните за заплатите на работниците
Според броя на дискретно разпределение може да се види, че същата характеристика стойност (варианти) се повтаря няколко пъти. Така x1 изпълнение се появява в комбинация два пъти, и Х2 вариант - 6 пъти, и т.н.
Ние изчисляваме средната заплата на един работник:
ТРЗ за всяка група е продукт на работни варианти на честотата (
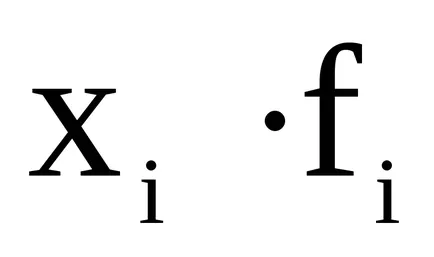
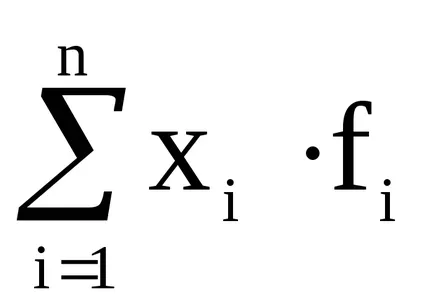
Ако изчислението е направено в съответствие с формулата и средната аритметична, средните доходи са равни на 3000 рубли. (). Сравнявайки този резултат с първоначалните данни, очевидно е, че средната работна заплата трябва да бъде значително по-висока (повече от половината от работниците получават заплати по-високи от 3000 рубли.). Ето защо, при изчисляването на средната аритметична в такива случаи би било грешка.
Статистическа обработка на материала в резултат може да бъде представен не само като серия от дискретни разпределение, но също така и под формата на интервал вариант серия със затворени или отворени интервали.
Помислете средната аритметична стойност за тази серия.
Пример 3. Таблица 3