Признаци на тригонометрични функции - studopediya
Функцията знак тригонометрични зависи единствено от координират тримесечие, което е числов аргумент. Последният път, когато се научи да превежда аргументите на Радиан мярка градуса (вж. Урок "Радиан и степен мярка на ъгъла"), а след това се определи най-координират тримесечие. Сега ние ще, в действителност, определянето на задължително плоча, косинус и тангенс.
синуса на ъгъла # 945; - координатна (координатната у) точка на тригонометрични кръг, който се появява, когато радиус на завиване на ъгъл # 945; ,
косинус на ъгъла # 945; - е абсцисата (координата х) точка на тригонометрични кръг, който се появява, когато радиус на завиване на ъгъл # 945; ,
На допирателната на ъгъла # 945; - съотношението на синуса на косинус. Или това, което е едно и също, съотношението на Y-координата на координатната х.
Всички тези определения са ви познати от гимназията Разбира алгебра. Въпреки това, ние се интересуват не притежавате дефиниция, и последиците, които възникват на тригонометрични кръга. погледнете:
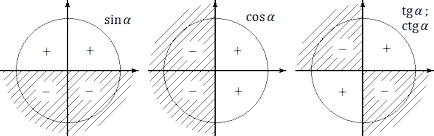
Blue цвят показва положителна посока OY ос (ордината ос), червени - положителни ос посока OX (абсциса). В този "радар" признаци станат ясни тригонометрични функции. По-специално:
1. грях 945 #> 0, ако ъгълът # 945; Тя се намира в I или II координира тримесечие. Тя proiskhoditiz факта, че по дефиниция синуса - е абсцисата (координата у). А координира Y е положително точно координира I и II четвърти;
2. защото 945 #> 0, ако ъгълът # 945; Той се намира в I или IV координира тримесечие. Тъй като само tamkoordinata х (известен още като - абсцисата) е по-голяма от нула;
3. TG 945 #> 0, ако ъгълът # 945; е аз или III в квартал координира. От това следва от определението: за TG # 945; = Y. х. така че това е положителен само когато х и у са същите знаци. Това се случва в I координира четвърт (където х> 0, у> 0) и III четвърт координира (х <0, y <0).
За по-голяма яснота, ние отбелязваме признаци на всеки тригонометрични функции - синус, косинус и допирателни - в някои "радар". Ние получаваме следната картина: