Нещо за огъване на релси

Близките забележителности. Ако трябва да пътуват на борда на влаковете по железопътната, а след това погледнете в релсите Може би се чудите как точно те са закръглени. Става дума за това, което се случва с влак в права линия, а след това започва да се обърнат - как? Въпросът не е съвсем тривиално. За да започнете да ме напомня някаква информация от хода на физиката. Силата действа върху тялото (например, вагон) е пропорционален на масата на времената на тялото на ускорението, с която се движи тялото. Аз специално написа текста, както следва: като че напротив, промяна на причината и следствието, както ще говорим за не-инерциална референтна рамка. Ясно е, че ако ние говорим за бутане шейни върху леда, че е необходимо да се каже, че в резултат на приложената сила шейна започват да се ускори. Но когато става дума за пътник, който пада от рафта заради внезапното спиране на влака, а след това има и друг начин: тази невидима сила, която бутна на пътника, причинено от ускорението на влака, в който пътникът е бил. Така че, в първите дни на железниците, когато скоростта на влаковете са малки, въпросът за това как да се развие в ъглите на пистата не е толкова от значение. Можете просто да се направи пряко преход от железопътния към железопътен транспорт, който е част от кръга до желания радиус на завиване R0.

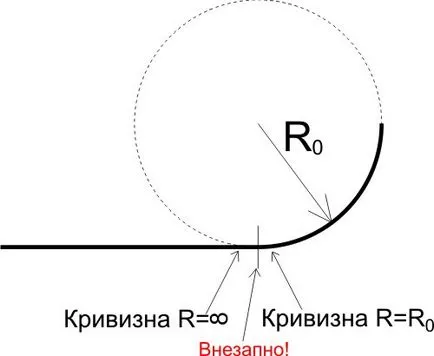
Въпреки това, този подход е опасно, защото при движение по такъв железния път по време на преход от директна железопътна до доста силно заоблени във влака започва да действа строго центробежна сила. Това означава, че в действителност при движение по крива, като удар срещу страната. Позволете ми да ви напомня, че центробежната сила е равна на:

(1)

където - скоростта на влака, - радиусът на кривината. I се отбележи, че радиусът на кривина на извивката (кривината = 1 / радиус на кривината) - концепции са приложими не само в кръг, но като цяло да е сложна крива. В произволна крива, за разлика от радиуса на периферната кривина е различен за различните точки на кривата. Как да се намери радиусът на кривината на произволна точка на кривата? Ние трябва да се вземат двете точки (червени точки в графиката по-долу) на кривата до нас желания (жълто), преминавате през тези точки допирателната (червен) към кривата, а след това през една и съща точка на перпендикулярно (в синьо) до допирателната. Разстоянието от точката на пресичане на перпендикуляра към крива (зелена линия) и радиусът на кривината ще бъде.

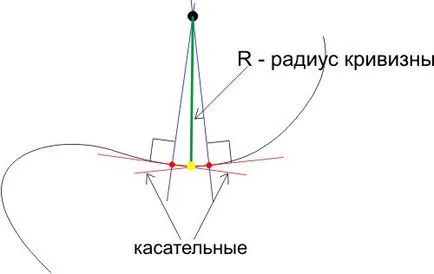
Разбира се, читателите не са запознати с диференциала смятане може да се зададе въпросът: за какво точно точката на кривата (в жълто на фигурата) е необходимо да се измери разстоянието от пресечната точка на перпендикулярите? Отговорът е, че ако разстоянието между червени точки (точките, в които провеждаме, допирателна към кривата) клони към нула, а след това можем да вземем като жълта точка на кривата на някой от червените, тъй като те са и трите ще бъде безкрайно близо един до друг. Така, че е този радиус на кривината е включен във формулата (1) за центробежната сила. И от там се вижда, че в продължение на една права линия, която има безкраен радиус на кривина, центробежната сила е равна на нула. Това е, когато един влак се движи по прав път, рязко се превръща в дъга, ние получаваме зависимостта на центробежна сила от време на време:

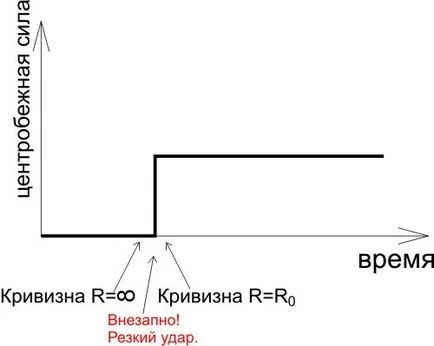
Това може да се види, че силата идва внезапно. И това е лошо, внезапна сила на председател се нарича удар, удар, може значително да се залюлее колата и да предизвика катастрофа. Ето защо, когато полагането на релсите направя така, че центробежната сила при движение, което се разраства постепенно в крива:

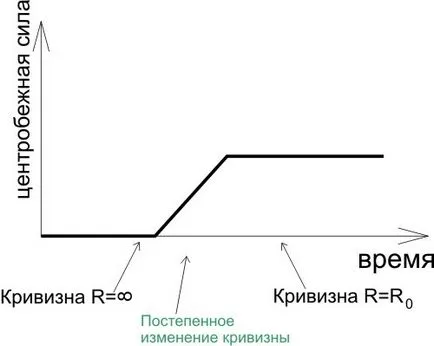
Това означава, че между прав участък с безкраен радиус на кривина и дъгата прави преход крива на окръжност, чийто радиус на кривината варира от безкраен да ограничен. Например, тя може да бъде крива, която се дава с израз на формата: който е апроксимация на кривата, която се нарича "клотоида". Клотоиди - е крива, в която кривината (кривина =) пропорционално на изминатото разстояние (когато въртите волана се върти с постоянна скорост). Оказва автомобилни магистрали също прави за клотоида се, според Уикипедия, като позволява преминаването на такива завъртания с малко или никакво намаляване на скоростта.

Това е начинът, по mat.analiz и диференциална геометрия са полезни за икономиката 🙂

Ако сте харесали на материала, моля да го споделите с приятелите си:

Няма сродни служби