Намалена въртящ момент и понижено инерционен момент

Условно въртящ момент се прилага за връзката на шофиране, се нарича движеща въртящ момент (сила даден момент). Движеща сила на въртящия момент е равен на сбора от всички моменти и сили, приложени към връзките на механизма. Намалена момент М. движещи сили, приложени към връзката задействащ се определя от равнява моментните сили. Силата разработен от М. е равен на сбора на властта, разработена от силите и моментите на силите, действащи върху връзките на снимачната площадка на машината.

Условно инерцията шофиране единица се нарича намалява инерционния момент. За всяка позиция на механизъм намалява инерционен момент единици се изчислява по формулата:

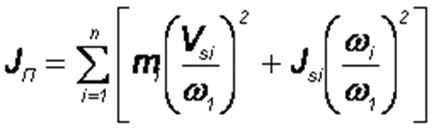
къде ми - маса на линк аз. ИУСС - инерционен момент свържа около ос, минаваща през центъра на масата на ниво Si, Wi - ъглова скорост на връзката и. Вси - центъра на масата скорост на връзката и.

Даден момент се нарича сили момента (MNR), прикрепени към връзката за задвижване и развива мощност, равна на капацитета на сумата от всички сили и моменти от сили, приложени към връзките на механизма.

InertsiiJnp намалена момент е инерционният момент на шофиране единица като кинетична енергия, равна на сумата от кинетичната енергия на всички движещи се части на механизма.

1. Уравненията на движение на машината намира в формите на енергия и диференциал.

За да се определи законите за движение на първоначалните връзките на дадените сили използват уравнения, наречени уравненията на движение на механизма. Броят на уравненията е равен на броя на степените на механизъм мобилност.

уравнения Механизъм за движение могат да бъдат представени в различни форми. За механизми с една степен на свобода е един от най-простите форми на уравненията, получени въз основа на теоремата за изменение на кинетичната енергия: кинетична механизма за изменение на енергията върху движеща работа е сумата от всички сили, които действат върху връзките за механизъм на този много движи. Това право уравнение като: T-T0 = ΣA (1), където Т - кинетичната енергия на механизма в произволна позиция; T0 - кинетичната енергия на механизма в положение, което се приема като първоначалните; ΣA - сума от работата на всички сили и моменти, които се прилагат за механизма на действие. Работа, извършвана всички активни сили и моменти и сили на триене във всички кинематични двойки на механизма. Уравнението на движение под формата на енергия. Ние намаляваме всички механизъм сили и моменти с една степен на свобода на един строеж връзка, т.е. замени този механизъм на неговия динамичен модел. От целия товар се прилага за модела, изразена издигнат момент мСв. дясната страна на уравнение (1) е равно на:

а именно, уравнение (1), като се има предвид, че може да се запише като

Уравнение (3) се нарича уравнението на движение на механизма под формата на енергия, или - под формата на кинетична енергия уравнение.

Уравнението на движение на механизма за диференциално включва втори път производни на координати. кинетичната енергия на механизма на промяна е равна на стъпката на работата на силите, действащи върху механизма:

Ако основният връзката извършва въртеливо движение :. след това