Момент на инерция, fizportal
инерционен момент
За изчисляване на инерционен момент ние трябва психически разделят тялото в достатъчно малки елементи, точки, които може да се счита да лежи на същото разстояние от оста на въртене, а след това намери произведението на масата на всеки елемент от квадрата на разстоянието от оста, и най-накрая да обедини всички получения продукт. Очевидно е, че това е един много отнемаща време задача. да брои
инерционни моменти на телата с правилна геометрична форма, можете да използвате в редица случаи, методите на интегралното смятане.
Намирането краен сбор от инерционни моменти на елементите на тялото заменят сумиране безкрайно голям брой инерционни моменти, изчислени за безкрайно малки елементи:
огра = 1 ∞ σδmi ри 2 = ∫r 2 дм. (В δm → 0).
Изчисляваме инерционният момент на единна твърда диск или височина цилиндър ч спрямо неговата ос на симетрия
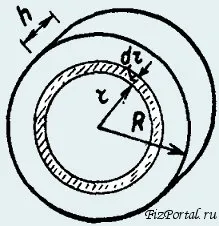
Dismember устройство на елементите във формата на тънки концентрични пръстени, центърът на оста на симетрия. Полученият пръстен има вътрешен и външен диаметър г р + р. и височина ч. От д-р <
I = σδmr 2 = R 2 σδm.
където σδm - масата на целия пръстен.
Обем 2πrhdr пръстен. Ако плътността на диск материал стр. След това масата на пръстени
ρ2πrhdr.
Инерционният момент на пръстена
I = 2πρhr 3 др.
За да се изчисли инерционният момент на целия диск, е необходимо да се обобщи моменти на инерция на пръстените от центъра (г = 0) до ръба (R = R), т.е. изчисли интеграла ..:
I = 0 2πρh R ∫r 3 др.
или
I = (1/2) πρhR 4.
Но диск тегло М = ρπhR 2. следователно
I = (1/2) Г-н 2.
Нека (без изчисляване) моментите на инерцията за някои органи с правилна геометрична форма, изработен от хомогенни материали
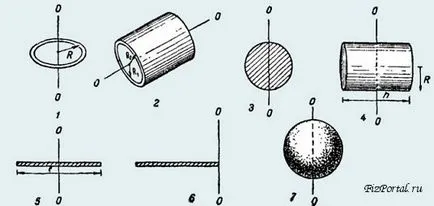
1. инерционният момент на тънък пръстен около ос, минаваща през центъра и перпендикулярна на неговата равнина (или тънкостенни кух цилиндър спрямо нейната ос на симетрия):
I = т-2.
2. момент на инерция на дебелостенна цилиндър по отношение на оста на симетрия:
I = (1/2) m (R1 2 - R2 2)
където R1 - вътрешен и R2 - външен радиус.
3. инерционен момент на задвижващите ос съвпада с един от неговите диаметри:
I = (1/4) Г-н 2.
4. момент на инерция на твърд цилиндър по отношение на една ос, перпендикулярна на образуващата и удължаване чрез средата:
= I m (R 2/4 + Н 2/12)
където R - радиус на основата цилиндър, з - височината на цилиндъра.
5. момент на инерция на тънък прът около ос, минаваща през средата му:
I = (1/12) 2 мл.
където L - дължина на пръта.
6. инерционният момент на тънък прът около ос, простираща се през единия си край:
I = (1/3) мл 2
7. момент на инерция на топката спрямо ос съвпада с един от неговите диаметри:
I = (2/5) Г-н 2.
Ако известен инерционен момент на всеки орган по отношение на оста, минаваща през центъра на масата, инерционен момент на всяка ос, успоредна на първата, може да се намери на основата на така наречената теорема Хюйгенс-Щайнер.
Инерционният момент за всяка ос I е моментът на инерция Ic тялото около ос, успоредна на това, минаваща през центъра на масата на тялото плюс м тегло. умножена по квадрата на разстоянието L между осите:
I = Ic + мл 2.
Като пример се изчисли инерционният момент на сферата с радиус R и маса м. резба суспендира с дължина L, около една ос, минаваща през точка О. преждата маса суспензия е малък в сравнение с масата на топката. От момента на инерция около ос, минаваща през центъра на масата на Ic = (2/5) Г-н 2. разстояние
между осите (L + R), инерционният момент около една ос, преминаваща през точката на окачване:
I = (2/5) Г-н 2 + m (L + R) 2.
Размерът на инерционния момент:
[I] = [М] х [R 2] = ML 2.