махало

Целта на тази работа е: проучване математическо махало (в зависимост проучване период на колебание от дължината на математическото махало и маса) и определяне на ускорението на нейната средна свободно падане чрез въртящ се махало.

2. Теоретична въведение

2.1. Математически махало математическо махало се нарича идеализирана система, състояща се от безтегловност и неудължаващ резба, който се суспендира маса концентрира в една точка. Сравнително добро приближение-zheniem математическата махалото е устройство, което представлява малък ING тежка топка спряно на дълга тънка нишка (фиг. 1).

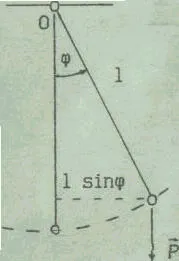
Отклонението на махалото от равновесното положение ще бъде функции, плътността на ъгъл

, образува нишка с вертикалата. Махалото в действия на външни сили: гравитациятаи реакцията на суспензията ос 0. В случай на махалото от равновесното положение, има момент на силаспрямо оста 0, с тенденция към връщане на махалото подаването на равновесие. Ако силата лежи в равнина, перпендикулярна на тази ос, неговият момент около тази ос е равен по сила на произведението на рамото на сила (разстоянието от оста на линията, по която сила действа). Когато махалото се завърта на ъгълв една посока на силатаима тенденция да се върти в обратната дрямка-систематичен начин. Следователно знака на момента на силапо отношение на ос О е противоположна на ъгъла на завъртане на махалотоISIN.

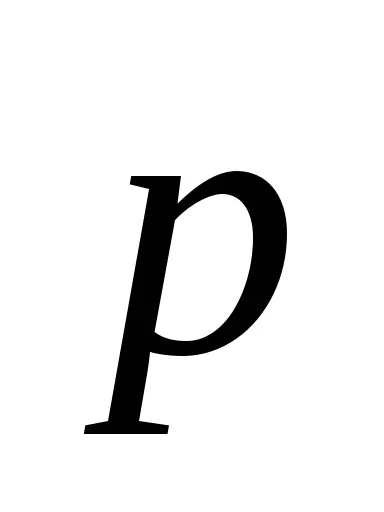
Изразът за въртящ момент М прилага Mayat-участника е на формата

където m - маса на махалото;

Б - земно ускорение;

мг - тежестта (Р = мг);

1 - дължина на махалото.

Стойност 1 грях

- рамо на сила F спрямо оста 0.

За проучване на колебание на махалото трябва да използва основния закон на динамиката на въртеливото движение

където J - инерционен момент около оста на въртене 0;

д - ъгловото ускорение на тялото (е = г 2

/ Dt 2. т - време);

М - получената момент (алгебрична сума от всички моменти, които действат върху тялото на външни сили спрямо оста 0). Момент на инерция J, че играе същата роля-Kuyu време на въртеливото движение на тялото, което маса в превод, т.е. Това е мярка на инерционния тялото по време на въртеливото движение, и характеризира раси ПРЕДЕЛЕНИЯ-масата на обема на тялото.

Инерционният момент около оста на масата на материална точка е продукт на точките на квадрата на разстоянието г от оста

За удължени тела на инерционен момент се определя като сумата от моменти на инерция на отделните елементарни масите Δmi, които могат да бъдат разделени на тялото, т.е.

където интеграл се простира върху целия обем на тялото.

Инерционен момент спрямо оста на математически махало окачване 0. съгласно формула (3)

Като се има предвид стойностите (1) и (5) от основния закон на динамиката (2) е под формата на махало "

Разделяне двете страни на уравнение (6) в 2 мл и въвеждане на наименованието

Ние се получи диференциално уравнение на колебание на математически ma-yatnika

Уравнение (8) не може да се интегрира по отношение на времето с помощта на елементарните функции. Ето защо, ние се ограничаваме само до малките трептения махало, с изключение на греха

След това, вместо 0 (8) ще имаме следната приблизителна диференциално уравнение за малките колебания на махалото:

Общият разтвор на това уравнение има формата

където А и А - са произволни константи определят от първоначалните условия на движение.

Големината А, т.е. най-голямата стойност на ъгъла на отклонение от вертикалата на махалото, амплитудата на колебание се нарича, - грях

на - цикличен честота (,V - честота на трептене), аргументът () - F Зоя трептене, и количеството- първоначалните колебания фаза (фаза зададени стойности на първоначалното време, т.е. при Т = 0).

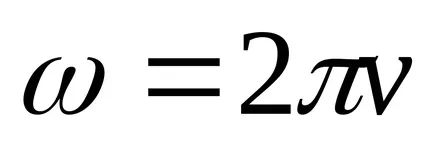
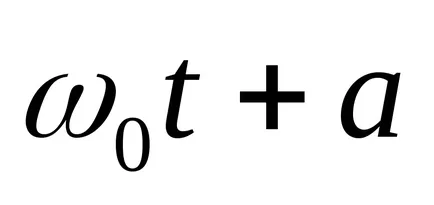
По този начин, за малките трептения на ъглово отклонение на Актуално ma махало се променя с времето в зависимост от хармоничен закон. Под голям ъгъл на отклонение на махалото ще изпълнява комплекс колебателно движение. Както следва от уравнение (7), честотата

за малките колебания на махалото зависи от дължината си и върху ускоряването на свободно падане и не зависи от масата на махалото. Периодът на малките трептения на математическо махало, ако смените има стойност (7) се определя по формулата

Периодът на колебание на махалото при малки амплитуди не зависи от амплитудата. Това свойство се нарича изохронни трептения махало (открит от Галилео - през 1583).

Физическа махало наречен твърдо тяло, което може да се върти (люлка) около фиксирана ос под действието на 0-проп Твен тегло (фиг. 2).

Помислете колебания по отношение на формата и разположението на карта-ционни елементи на масата на махалото. На махалото се отби от равновесието на пут-ТА, в действия на външни сили: гравитацията

и реакцията на суспензия ос 0. триене в пренебрегване ос. оста Реакционната суспензия не момент около оста на въртене. Момент, който се стреми да се върне махалото към равновесното си положение, е

,

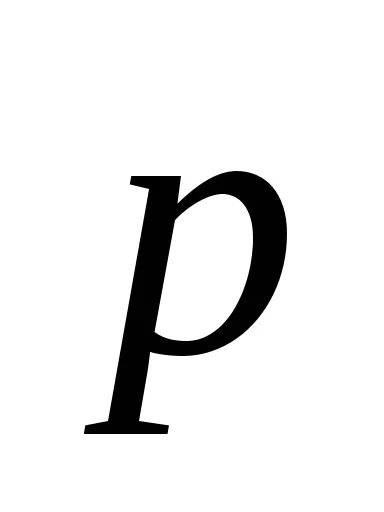
където m - маса на махалото;

1 - разстоянието между точката на окачване 0 и центъра на масата mayatni Единична S.