Линейни хомогенни втори ред диференциални уравнения с постоянни коефициенти,
В тази статия ще разгледаме принципите на разтвора на линейни хомогенни втори ред диференциални уравнения с постоянни коефициенти, където р и р - са произволни реални числа. Първата спирка на теорията, а след това се прилага резултатите при решаване на примери и задачи.
Ако ще се натъкне на непознати термини, които се отнасят до определения и понятия от теорията на диференциалните уравнения.
Нека формулираме теорема, която определя вида, в който да се намери общо решение на линейни обикновени диференциални уравнения.
Общият разтвор на хомогенна линейна диференциално уравнение с непрекъснато върху интервала на интеграция се определя от комбинация коефициенти X линейни, при което - линейно независими специално разтвори за линейни обикновени диференциални уравнения и X. - произволни константи.
По този начин, общото решение на хомогенна линейна втори ред диференциално уравнение с постоянни коефициенти на формата на y0 = C1 ⋅Y 1 + С2 ⋅y2. където Y1 и Y2 - частни линейно независими решения, и С1 и С2 - произволни константи. Остава да се научите как да се намери конкретен решения Y1 и Y2.
Euler предложи да се търсят конкретни решения във формата.
Ако вземем конкретно решение на линейни обикновени диференциални уравнения от втори ред с постоянни коефициенти, уравнението, което трябва да се получи идентичност чрез заместване на това решение:

Така че ние имаме така наречената характеристика уравнението на линейна хомогенни от втори ред диференциални уравнения с постоянни коефициенти. Решения k1 и k2 на характерното уравнение определи конкретните решения и нашите линейни обикновени диференциални уравнения от втори ред с постоянни коефициенти.
В зависимост от коефициентите P и Q са корените на уравнението характеристика може да бъде:
- реално и различно,
- валидно и за съвпадение,
- комплекс конюгат двойка.
В първия случай, специално разтвори са линейно независими от първоначалното диференциално уравнение и са общото решение линейни обикновени диференциални уравнения от втори ред с постоянни коефициенти са.
Функции и наистина линейно независими, тъй като Wronskian не е нула за всяко реално х за.
Във втория случай, един конкретен разтвор е функция. Във втори специално разтвор се смесва. Ще покажем, че наистина конкретно решение на линейни обикновени диференциални уравнения от втори ред с постоянни коефициенти и да докаже, линейна независимост на Y1 и Y2.
Тъй k1 = k0 и k2 = k0 съвпада корени на характеристика уравнението, то има формата. Следователно - начална хомогенна линейна диференциално уравнение. Заместник в нея и да се уверите, че уравнението става за самоличност:
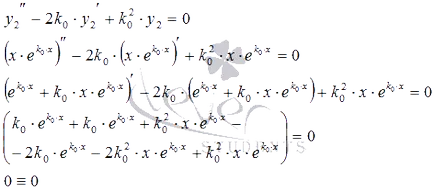
По този начин, особено разтвор на първоначалното уравнение.
Ние показваме линейна независимост на функциите и. За да направите това, ние се изчисли Wronskian и се уверете, че то е различно от нула.

Заключение: линейно независими специално разтвори на линейни обикновени диференциални уравнения от втори ред с постоянни коефициенти са и и общото решение е.
В третия случай, ние имаме няколко сложни и частни решения на линейни обикновени диференциални уравнения. Общото решение се изписва така. Тези конкретни решения могат да бъдат заменени от две реални функции и съответните реални и въображаеми части. Тя може да се вижда ясно, ако конвертирате общо решение, като се използват формулите от теорията на функциите на комплексна променлива тип:
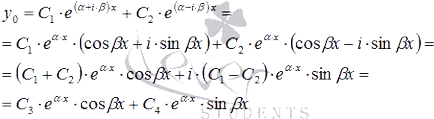
където В3 и В4 - произволни константи.
Така че ние се обобщи теорията.
Алгоритъмът за намиране на общ разтвор на хомогенна линейна втори ред диференциално уравнение с постоянни коефициенти.
- Ние напиши характеристика уравнение к 2 + р ⋅ К + р = 0.
- Намираме корените на характеристика уравнението на k1 и k2.
- В зависимост от стойностите на корените на характеристика уравнението е общото решение на линейни обикновени диференциални уравнения с постоянни коефициенти под формата на:
- , ако;
- , ако;
- , ако.
Помислете примерите за всеки отделен случай.
Виж общия разтвор на хомогенни линейни втори ред диференциални уравнения с постоянни коефициенти.