Лекция 2 непредубедени, и последователни оценки на ефективни параметри разпределителните

За да се даде статистически оценки добро приближение на определените параметри, те трябва да бъдат безпристрастно и ефективно богати.

Безпристрастен нарича статистическа оценка

параметър, математическото очакване е равна на прогнозната параметър за всеки обем на пробата.

Тя измества нарича статистическа оценка

параметър, очакването, което не е равна на прогнозната параметър.

Ефективно нарича статистическа оценка

параметър, който за даден обем пробаТой има най-малката вариация.

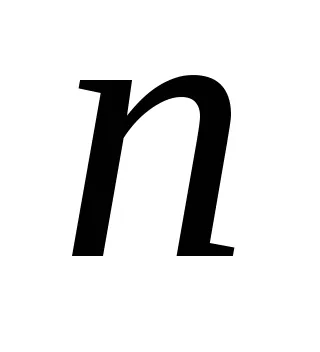
Заможните нарича статистическа оценка

параметър, че когатотенденция в вероятност на изчислената параметър.

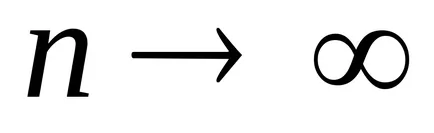
За се получават проби от различни размери на различните стойности на средната аритметична и статистическа дисперсия. Ето защо, статистическата стойност и дисперсията са случайни стойности, за които има очакване и дисперсията.

Ние изчисляваме очакването и вариацията на средната аритметична стойност. Ние означаваме с

математическото очакване на случайна променлива

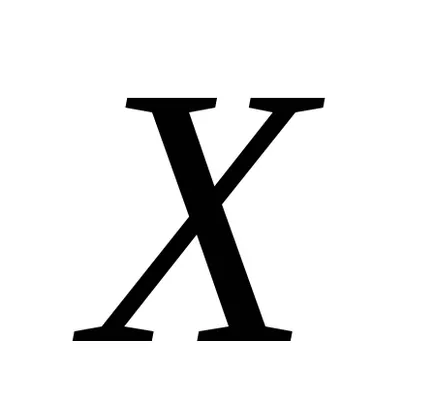
Тук, както и на случайни променливи се считат:

- SV чиито стойности са равни на първите стойностите, получени за различен размер на пробиот населението като цяло,-S.V. чиито стойности са втора стойности, получени за различен размер на пробиот населението, ...- SV чиито стойности са равни-м стойности, получени за различен размер на пробиот общото население. Всички тези случайни величини, разпространявани от същия закон и имат една и съща очакването.

.

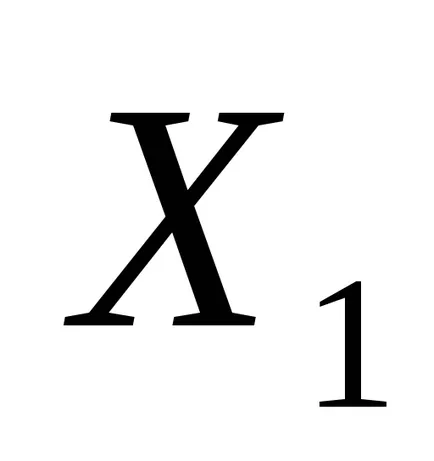
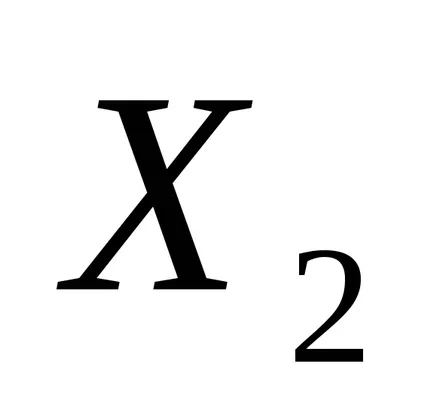
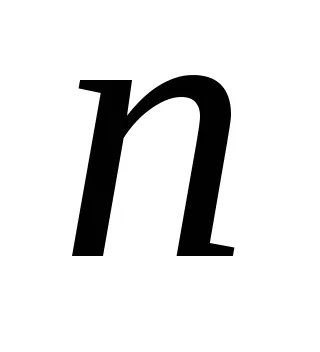
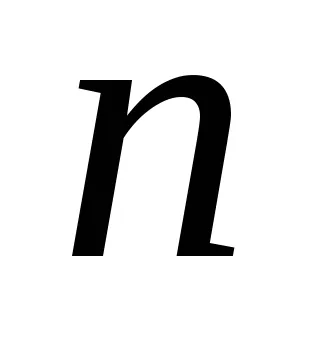
От формула (1), че средната аритметична е обективна оценка на очакването, защото математическата очакването е равен на средната аритметична величина на математическото очакване на случайна променлива. Тази оценка е в съответствие. Ефективността на тази оценка зависи от вида на случайна променлива разпределение

. Ако, например,нормално разпределение, оценка на очакването за използване на средната аритметична стойност ще бъде ефективна.

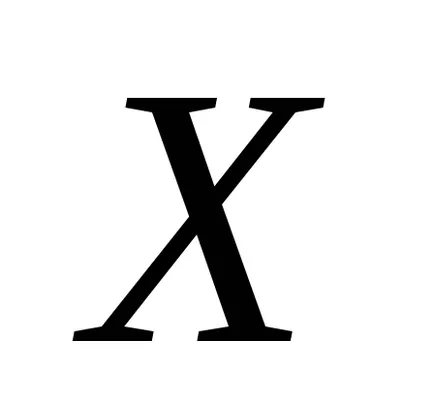
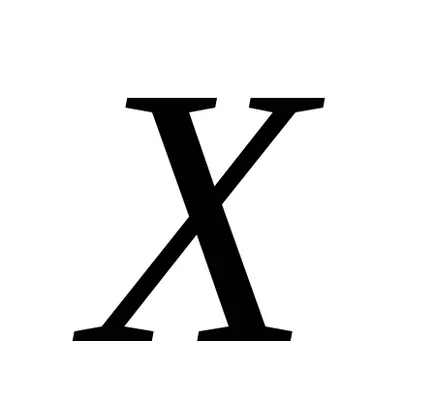
Сега ние откриваме статистическата оценка на дисперсията.

Изразът за статистическа дисперсия може да се превърне, както следва:

Сега ние откриваме, очакването на статистическа дисперсия

От формула (6) показва, че очаква статистическа дисперсия се различава с коефициент на дисперсия, т.е. Това е предубеден оценка на дисперсията на населението. Това се дължи на факта, че вместо истинската стойност

, който е неизвестен, средната статистическа се използва в дисперсията на оценката.

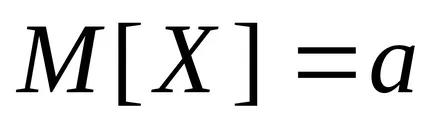
Ето защо, ние се въведе актуализирана статистическа вариация

Тогава очакването на ревизирана статистическа вариация, равна

т.е. се коригира статистическа вариация обективна оценка на дисперсията на населението. Получената оценка е в съответствие.