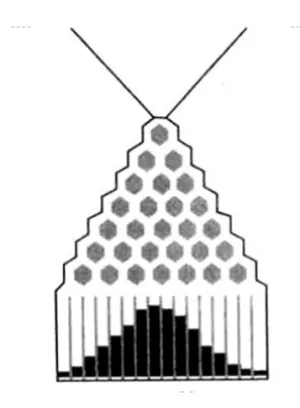
крива на Гаус

В основата на сдружение на вероятностите и статистиката са две забележителни факти. Един от тях - явление на статистическа стабилност. Второто е, че в много, различни по своята същност статистически наблюдения статистическа стабилност може да бъде описан от една функция. Тази функция е въведена от големия немски математик Karlom Gaussom (\ (1777-1855 \)). Тя се дава много сложна формула:

ϕ (X) = 01 февруари π д - х 02 февруари

Графиката на у = ϕ (X) нарича Gaussian крива. Това е "камбанка" крива. Той има един-единствен максимален точка симетричен по отношение на ординатната ос, площта под кривата равна на единство. Тя бързо асимптотично подходи х-ос:

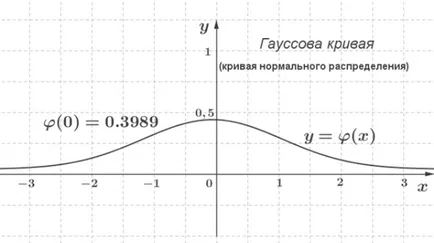
Esli оценка на площта под кривата Gaussian в интервала - 3; 3. да получите \ (0.99 \), т. Е. Повече от 99% от площта.

Хистограми на разпределението на голямо количество информация са необходими в случаите, когато броят на данни се състои от много голям брой числа. Ако ширината на вертикалните колони на хистограмата е достатъчно малък, а основата колона заедно оставя определен интервал, след това хистограмата се е подобен на графиката на непрекъсната функция определя на този интервал. Понякога тази функция се нарича функция изравняване.

Графики изравняване на хистограмата функции, подобни един на друг. Всички тези криви на разпределение, получени от Гаусово крива. Това често се нарича нормално кривата на разпределение.

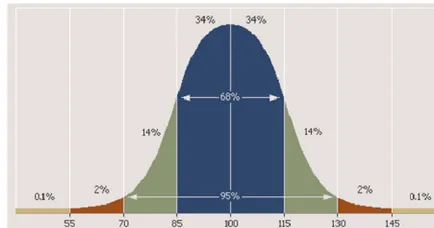
За да се демонстрира действието на закона за Гаусово разпределение понякога се използва специално устройство - един Галтън пансион (името на своя изобретател). В него подвижен в на върха на едни и същи топки са разпределени по движи между правилен шестоъгълник, в резултат на падане върху хоризонтална повърхност, образувайки картина, подобна на "подграф" камбана крива: