Кинематика на твърдо тяло
Абсолютно твърдо тяло се нарича тялото при шофиране е разстоянието между две фиксирани точки не се променя. Твърдо тяло може да бъде от двата вида - транслационни и въртене.
Когато движението напред на всяка линия, свързана неподвижно с тялото остава успоредна на първоначалната си посока и траекторията на две свързани с тялото, точките са идентични (те могат напълно да се приведе паралелно превод). Пример за постъпателно движение по отношение на земята може да бъде кабината на асансьора, "виенско колело" за пътниците, стрелката на компаса за произволна движи тялото му в хоризонтална посока и т.н.
По време на стъпката напред движение на радиус вектори на всички пиксели същия твърдо тяло и следователно същата скорост и тяхната ускорение. Следователно транслационно движение твърдо тяло е описан от кинематичните уравненията на някой от неговите точки.
Ако твърдо тяло въртенето на две точки А и В остане неподвижен, тогава всяка точка С лежи на една права линия AB също е фиксиран. Ако точка С се премества, за AC и BC сегменти на промени дължина, което противоречи на определението на твърдо тяло. А права линия, минаваща през сегмент AB се нарича оста на въртене. твърда движение тяло се нарича въртене на тялото около фиксирана ос.
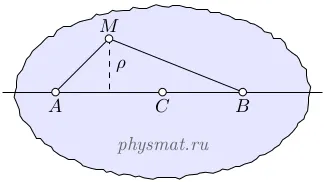
Фиг. 1 Абсолютно твърдо вещество
Да разгледаме произволна точка М на тялото не лежи на оста на въртене AB (Фигура 1). Тъй като дължината на УО на сегменти. MB и MN. където N пресечната точка на перпендикуляра спадна от точка М на оста AB. по време на движение остава постоянна, тогава всички точки на въртящо се тяло описва окръжност с радиус р, равно на разстоянието от точката на оста на въртене, в равнина, перпендикулярна на оста на въртене. Пример за въртене около фиксирана ос на ротора може да бъде електрически двигател или турбина.
Ако твърдо тяло фиксиран в една точка, неговото движение се нарича въртене на тялото около фиксирана точка. и то в момент, се нарича център на въртене. Когато такова движение може да определи моментално оста на въртене, като оста на въртене, простиращ се през центъра и перпендикулярна на равнината на движение. Позицията на моментната ос спрямо неподвижната рамка и тялото себе си може да се промени с времето.
За разлика транслационно движение, ротационно движение точки скорост об. разположени на различни разстояния от оста на въртене ще бъде различен. Следователно, по време на въртеливото движение скорост V отделна точка не може да служи като кинематичен характеристиката на движение на цялото тяло.
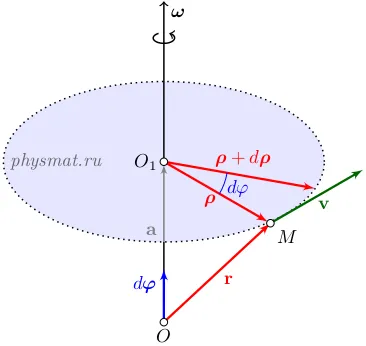
Фиг. 2 въртене твърдо тяло
Разглеждане на въртеливото движение на тялото спрямо ротационната центъра О с OO1 моментната ос на въртене. където точката O1 съответства на центъра на кръгова дъга, която се движи в точка М (Фигура 2). вектор радиус на точка М по отношение на центъра на въртене О е означена с R. радиус вектор от точка М по отношение на O1 обозначен с ρ. и вектор от точка до точка О O1 означават. Тези вектори са свързани с
За малък интервал от време DT ρ вектор се върти в равнина, перпендикулярна на ъгъл dφ оста OO1. вектор радиус на всяка точка на твърдо тяло (с изключение на точките върху оста, тъй като тяхното радиус вектор е нула) в DT време също се завърта от dφ ъгъл. в противен случай, това ще доведе до промяна и разстоянието между точките, което противоречи на определението на твърдо тяло. Оказва се, че dφ на ъгъла на завъртане характеризира въртеливото движение на тялото. Въвеждаме вектора на началното завъртане на тялото (малка ротация на тялото) dφ на. числено равно dφ на ъгъл на завъртане и насочена по OO1 оста. Посоката на този вектор съвпада с посоката на движение напред на палеца, дръжката се завърта заедно с тялото, т.е. подчинява правило дясна>.
Последователността на две елементарни завои dφ1 и dφ2. Освен вектор се подчинява на правилото, т.е. sumarno елементарни въртене е еквивалентен на един завой
Скоростта на изменение на ъгъла на завъртане φ наречен skorostyuω ъглова скорост и по дефиниция като съотношението на нарастване малък ъгъл в малко време DT са:
ъглова скорост вектор со на характеризира големината и посоката на изменение на ъгъла на завъртане. Ако ъгловата скорост е постоянна ω = конст. движението се нарича равномерно въртене около фиксирана ос.
скорост V на движение на точка М се наричат линейна скорост. Когато тялото се върти с ъглова скорост ω в точка време DT М преминава през кръгова дъга с радиус ρ път равна на DS. Линейната скорост е
Фигура 2 показва, че вектор линейна скорост е перпендикулярна на со вектори и р. и неговата посока съвпада с тяхната вектор продукт [ω. ρ]. Освен това, вектор со и р са взаимно перпендикулярни, така [ω. ρ] = ρω = об. Ето защо,
Оставен вектор со на. Като вектор ω лежат на една права и кръста си продукт е нула, получаваме
Ние счита за най-общия случай на въртене на тялото спрямо фиксирана точка - въртене центъра О. В конкретния случай, когато тялото се завърта по отношение на фиксираната ос, като точка О може да избере всяка точка, разположена върху оста на въртене.
За да се характеризира с равномерно въртеливо движение с помощта на поредица от понятия.- vrascheniyaT период нарича интервал от време, за който равномерно въртящи с ъглова скорост ω тяло извършва пълно завъртане, т.е. завърта на ъгъл φ = 2π.
- Vrascheniyaf честота е броят на оборотите на тялото, за 1 секунда при постоянна ротация на ъгловата скорост ω.
Тези количества са свързани, както следва:
Ако тялото върти неравномерно, тогава въвеждане на характеристика скоростта на промяна на ъгловата скорост - ъглово uskorenieε.
В случай на въртене на тялото около фиксирана ос, посоката на ъгловото вектор ускорение не се променя, но промените само неговата величина. Ε ъглово ускорение вектор е насочено по оста на въртене в посока на ъгловата скорост, ако стойността му е положителен (ускорено въртене) и в обратна посока на ъгловата скорост, когато стойността му е отрицателен (бавно въртене).
Ние експресира тангенциална и нормално ускорение произволна точка М на тялото, въртящ се около фиксирана ос чрез ъглови характеристики:
За векторни величини, следните зависимости:
Помислете за някои специални случаи на солидна ротация на тялото:- униформа въртене
Транслацията и въртеливо движение на твърдо тяло са най-простия вид движение. Като цяло, твърдото вещество може да изпълнява сложни волеви движения. В хода на теоретична механика е доказано, че всеки комплекс твърда движение на тялото може да се счита като сумата на транслацията и ротационни движения.
Позоваването- АА Detlaf, BM Jaworski, LB Milkovskaya. Физика разбира се. М. Висшето училище. 1973 година.