Как да формулира и да се докаже теоремата за уют

Формулирането и математически нотация

По този начин, косинус теоремата е формулиран, както следва:

Square страна на всеки триъгълник е равна на сумата от квадратите на другите две страни минус два пъти продукта на косинуса на ъгъла в страни, разположени между тях.

Разбира се, това е много време, но ако разбирате същността си, това е просто да си спомня. Един дори може да си представи един триъгълник чертеж. Визуално тя винаги е по-лесно за запомняне.

Формулата на този теорема ще бъде:

и 2 = 2 + 2 - 2 * в * а * защото А.

Малко по-дълго, но това е логично. Ако малко по-внимателно, ще видим, че писмата се повтарят, следователно, че е лесно да си спомня.

Една обща доказателство на теоремата

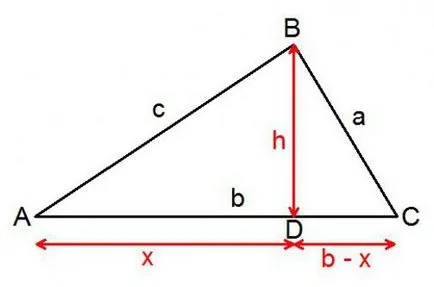
Както и да е вярно за всички триъгълници, можете да се откажете за всеки от типовете мислене. Нека това да бъде фигура с всички остри ъгли. Да разгледаме малък правоъгълен триъгълник, чийто ъгъл С е по-голям от ъгъла на връх В. Поради това голям ъгъл трябва да бъде намалена, перпендикулярна на противоположната страна. Прекарано височина ще раздели триъгълника на две прави. Тази нужда от доказване.

Страна се разделя на два сегмента: X, Y. Те трябва да бъдат изразени по отношение на известни количества. Частта, която ще бъде в триъгълника с хипотенузата равна на, изразена по отношение на протокола:

Друг ще бъде равна на такава разлика:

Сега ние трябва да напишете Питагоровата теорема за двама в резултат на изграждането на правоъгълни триъгълници, като височината на неизвестно количество. Тези формули ще изглеждат по следния начин:

N 2 = а 2 - (C * COS) 2,

N 2 = а 2 - (С - A * COS) 2.

В тези уравнения са едно и също изражение на ляво. Така че, тяхната дясна страни са равни също. Това е просто изгаряне. Сега трябва да се отварят скобите:

в 2 - 2 * (COS) 2 = а 2 - в 2 + 2 * A * COS а - 2 * (COS) 2.

Ако сте за извършване на миграцията, както и намаляването на подобни термини, ние получаваме първоначалната формула, която е написана след изявлението, че е теорема на уют. Доказателство за това е пълна.

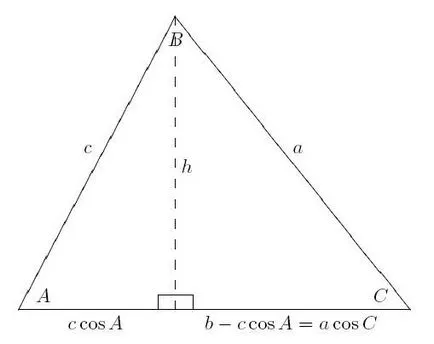
Доказателството на векторите

Тя е много по-кратък, отколкото предишната. И ако знаете свойствата на вектори, косинус теорема за триъгълник се оказа лесно.

Ако страните по един, B, C, означават съответно Vector VS, AS и AB, тогава имаме равенство:

Сега трябва да се извърши някакво действие. Първият от тях - е квадратура от двете страни на уравнението:

BC 2 = AC 2 + AB 2 - 2 AC * AB.

Тогава ще трябва да пренапише уравнението в скаларна форма, имайки предвид, че продуктът на два вектора е косинуса на ъгъла между тях в своите скаларни стойности:

BC 2 = AC 2 + AB 2 - 2 AC AB * A * защото

Остава само да се върнете към стария нотация и отново включите косинус теорема:

и 2 = 2 + 2 - 2 * в * а * защото А.

Формулите за другите страни, както и всички ъгли

За да намерите по посока на косинус теорема да се корен квадратен. Формулата за квадратите на други страни, ще изглеждат по следния начин:

2 = 2 + 2 - 2 * A * B * защото В.

За да напишете израз за квадратен страна да. Ние трябва да замени предишното равенство с A-те години. и обратно, и се поставя под ъгъл косинус В.

може да се изрази с косинуса на ъгъл от основната теорема с формула:

защото А = (2 + C 2 - 2) / (2 * и).

Подобно формули са получени за други ъгли. Това е добра практика, така че можете да се опитате да напишете своя собствена.

Разбира се, не забравяйте, че тези формули не са необходими. Достатъчно е да се разбере, теореми и възможността да се въвеждат тези прояви на господаря си.

първоначалната формула теорема ни дава възможност да се намери посока, ако ъгълът между двете не е известна. Например, трябва да се намери. когато се дават стойности: A, C, A или неизвестен с. но има стойност от А, В, A.

В тази ситуация, трябва да се движат всички условия на формулата на ляво. Вземи това равенство:

2 - 2 * A * C * защото A + 2 - 2 = 0.

го пренапише в малко по-различна форма:

2 - (2 * в * защото А) + C * (2 - 2) = 0.

Можете лесно да видите квадратно уравнение. Тя неизвестна величина - с. и всички останали, дадени. Поради това е достатъчно, за да се реши с помощта на дискриминантен. Така че ще бъде намерено неизвестно лице.

По същия начин, формулата за втората страна:

2 - (2 * е * защото А) * а + (с 2 - 2) = 0.

Сред другите изрази като формула твърде лесно да се получи за себе си.

Как да разберете, без изчисляване на косинус на вижданията на ъгъла?

Ако се вгледате внимателно в формулата на косинуса на ъгъла, получен по-горе, можем да видим следното:

• знаменател - винаги е положително число, тъй като тя е продукт на страните, които не могат да бъдат отрицателни;
• ъгъл стойност зависи от знака на числителя.

• остър в ситуации, когато числителя е по-голяма от нула;
• тъп, ако експресията е отрицателен;
• Direct, когато тя е равна на нула.

Между другото, последната ситуация привлича косинус теорема теоремата на Питагор. Защото за 90º ъгъл косинус е нула, а последният план изчезва.

Първата задача

Тъп ъгъл триъгълник е равен на произволен 120º. На страните, че е ограничен, като е известно, че един от тях по-голяма от другата, като 8 см. За трета дължина страна е 28 см. Необходимо ли е да се намери периметъра на триъгълника.

Първо трябва да се определи от едната страна на буквата "х". В такъв случай, а другият ще бъде равна на (х + 8). Тъй като има прояви на трите страни, можете да използвате формулата, дадена от косинус теорема:

28 февруари = (х + 8) х 2 + 2 - 2 * (х + 8) * х * защото 120 °.

Таблиците за уюта, за да откриете стойност, съответстваща на 120 градуса. Това ще бъде броят на 0.5 със знак минус. Сега разчита за отваряне на скобите, при спазване на всички правила и да се приведат тези условия:

784 = 16x + 2 х + х 64 + 2 - 2 * (0,5) * (х + 8);

2 = 784 2 + 64 + 16x + х 2 + 8x;

3 + 24x 2-720 = 0.

Това квадратно уравнение се решава чрез намиране на ограничения, не по който ще бъде равен на:

А = 24 24 * 3 * (- 720) = 9216.

Тъй като стойността му е по-голяма от нула, уравнението има два отговора-корен.

Последно корен не може да бъде отговорът на проблема, тъй като партията трябва задължително да бъде положителен.

Така че, са известни на двете страни. Това е лесно да се намери една трета: 12 + 8 = 20 (см). Сега можем да се отговори на въпроса на проблема. Периметърът на триъгълника се определя като сума от всички страни:

24 + 12 + 20 = 60 (см).

Отговор. периметър е 60 cm.

В триъгълника са известни: а. равно на 2 см; а. което е 10 см; Тъй като големината на ъгъла 120 °. Вие искате да намерите в страната.

Първо трябва да се възползват от косинус и се направи извод от това формулата на квадратно уравнение, което стойност не е известна:

2 = 2 + 2 - 2 * A * B * защото С

2 - (2 * а * защото С) * а + (2 - и 2) = 0.

Необходимо е да се заменят всички известни стойности в състоянието:

2 - (2 * 10 * 120 ° COS) * В + (2 10-2 2) = 0.

Сега трябва да се изчисли какво е възможно да се опрости израза:

2 - (20 * (-1/2)) * В + (100-4) = 0

2 + 10 * а - 96 = 0.

Това е стандартна квадратно уравнение, за да бъде решен чрез намиране на дискриминантата:

D = (10) с 2 - 4 * 1 * (-96) = 484.

Според формулите трябва да се направят изчисления за непознатата страна:

e2 = (- 10 - 22) / 2 = - 16 - не отговаря на това корен решаване на проблема, тъй като страната не може да бъде отрицателна.

A: неизвестна страна е 6 см.

Третата задача

В даден триъгълник страни: а, б, в. са съответно равни на 6 см, 10 см и 8 см. Изисква се изчисли ъгъл А.

Отново ще трябва да използвате теоремата за уют. Той използва протокола, който е косинус на ъгъл А, тъй като е необходимо да се изчисли. Това е написано правилната формула за косинус на ъгъла на неизвестното:

защото А = (2 + C 2 - 2) / (2 * и).

Остава да замени стойността на страните и да извърши всички изчисления:

защото А = (2 + 10 8 2 - 6 2) / (2 * 8 * 10).

След изграждането на всички условия в квадрата и размножаването на номера от знаменател:

А = COS (100 + 64 - 36) / (160).

След добавяне и разделяне се получава:

защото А = 128/160 = 0.8.

Сега трябва да използвате таблица Bradis, за да разберете каква е ъгъл А. Най-близката стойност на ъгъла за този косинус е 36º54 ".

A: Стойността на ъгъл А е 36º54 ".