Изчислени модел единици симулационни cistem автоматично регулиране Mathcad - част 2
Логаритмични честотни характеристики
В повечето случаи, характеристиките на амплитуда и фаза честота изобразени на логаритмична скала. Такива логаритмични честотни характеристики са много удобни за инженерни изчисления.
В конструкцията на логаритмичната амплитуда честота характеристика (LACHH) по протежение на оста на ординатата представлява стойността
Измерителната единица, за които децибели (db). По абсцисата ос W честотата на логаритмична скала (Фигура 8).
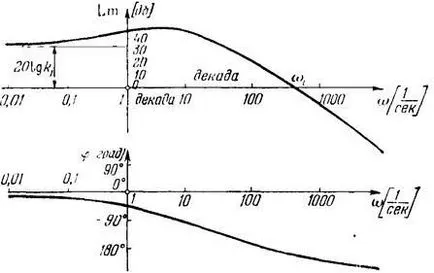
Фигура 8. Логаритмични честотни характеристики.
Еднакво елемент на х-оста е десетилетие - всеки сегмент, в който честота стойност се увеличава десетократно. В точката на пресичане с LACHH абцисата наречен WSr прекъсваща честота.
В конструкцията на логаритмичната фаза на честотата характерни (LPC) ъгли броят Y е вертикалната ос в нормално скалата в ъглови градуси. На абсцисата се нанасят по честота W остава в логаритмична скала.
Важно е да се има предвид, че абсцисата (L = 0) съответства на стойност к = 1. т. е. преминаване през амплитуда връзка сигнал без промяна на амплитудата. LACHH горната половина равнина съответства на стойности на к> 1 (амплитуда печалба) и долната половина равнина - стойностите на А<1 (ослабление амплитуды).
2. Основните видове единици.
Видове единици на автоматични системи за контрол и регулиране се различават в зависимост от вида на функции за трансфер (или диференциални уравнения), които определят техните динамични свойства и характеристики.
Типични единици се характеризират с динамични диференциални уравнения на за не повече от два.
В зависимост от вида на диференциални уравнения в теорията на автоматичното управление се прави разграничение между следните основни видове връзки:
-inertialess (пропорционално или усилвателна);
-инерционни първи ред (или апериодична);
-инерцията на втори ред;
Основните видове връзки са разделени на три групи:
Позиционни единици са тези, в които предавателната функция
Полиноми Bm (п) и (р) са постоянни условия, равни на 1, т.е., тези връзки са статични характеристика Yust = к х Хуст (при Р = 0W (р) = к =), определя тяхната равновесно състояние - .. позиционно имот ,
В диференциране елемент в експресията на предавателната функция не е константа на числителя, т.е. веднъж за диференциране елемент ще B0 = 0 ..:
Когато Bm-1 (р) е постоянно Терминът равно на 1, и К = - печалба.
Функциите прехвърлянето на интегриране на компонента са, съответно:
Когато-1 (п) има свободен Терминът равна на 1.
Познаването на типичните характеристики на единици, необходими за системи за управление на плащане.
2.1. Идеален усилвателна (inertialess) връзка.
Уравнение и нивото на предавателната функция:
Примери са свободен ход редуктора, делител на напрежение, сензори ъгъл, моментната мощност и сътр. (Фиг.9).
Фиг. 9. Примери свободен ход единици.
В действителност, не свободен ход единици. Обикновено се счита идеален единици ОСП инерцията е много по-малък от инерцията на останалите връзки. Повечето случаи на различни датчици и предусилватели. Инерционно забавяне на много измервателни елементи на автоматични системи (ъгъл разминаването сензори, фотоелектрически сензори, датчици магнитно) е малък, така че те се считат inertialess връзки.
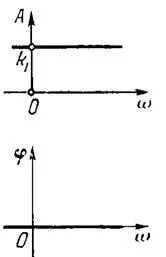
Фигура 10. характеристики на честота свободен ход единични
2.2. Инерционни (апериодична) връзка.
Уравнение и нивото на предавателната функция:
Когато Т - времеконстанта; K - скорост на предаване на връзката.
Примери на инерция (апериодични) единици са двигатели за постоянен ток, когато X (т) - захранващо напрежение, и Y (т) - ъгловата скорост на W на вала (т); двуфазни асинхронни двигатели; Усилватели с инерционно забавяне предвид; масивно тяло, ако променливата вход да брои броя на входящите топлина за единица време и изходния Q. - температурата във всяка точка вътре в тялото, и т.н.). L-R верига (Фигура 11).
Фигура 11. Пример инерционни връзка.
Фигура 12. APFC инерционно елемент.
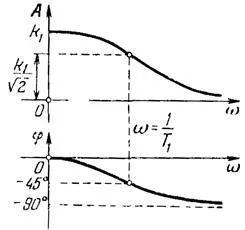
Фигура 13. амплитуда честота и фаза отговор на инерционно единица
логаритмичната амплитуда честота характеристика има формата:
Тази характеристика има асимптота:
Последно асимптота е наклонена права линия с наклон от -20 db / десетилетие, както и първата - хоризонталната линия. Асимптоти се пресичат в точка Wc =. Самата LACHH близо до тези асимптоти.
На логаритмична мрежа в честотата ос честота ъгъл Wc = (Фиг.14). За честоти по-малко от чифтосване, т. Е. Когато W<. можно пренебречь вторым слагаемым под корнем, тогда левее сопрягающей частоты можно заменить L(W) приближенным выражением
Този израз съответства на хоризонталната линия. За честоти голяма чифтосване W> в експресията на L (W) може да се пренебрегне 1 при корена. След L (W) = 20lgk-20lg (WT). Вторият план е права линия, простираща се под наклон -20 db / десетилетие. Прекъсната линия се нарича асимтотична LACHH. Най-голямото отклонение от точната LACHH асимтотична приблизително 3 db при честота от спрежение, т.е. да..:
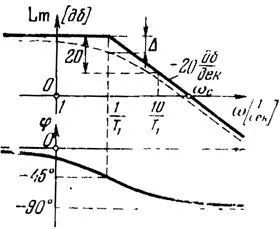
Фигура 14. LACHH инерционно елемент.
Функцията преход, съгласно решение единица уравнението за X (т) = 1 (т) и нула първоначалните условия е (Фиг.15) на:
Фигура 15. Функцията преход на инерционно единица.
Времевата константа определя наклона на допирателната Т в началото на кривата (Фигура 15). Следователно, стойността на Т характеризира нивото на устойчивост, т.е.. Е. Продължителността на преходни. На теория, този процес на преход трае неопределено време. На практика тази връзка в преходно време разбираме периода от време, след което Ц. неравенството:
Когато се прилага към входния сигнал Х0 DC връзката След преходно координира Y (т) е неподвижно свързан с входа:
2.3. Трептящо единица.
Уравнение и нивото на предавателната функция:
Общоприето запис на предавателната функция на вибрационното ниво под формата на:
Амплитуда и честота отговор фаза (Фигура 16) връзка:
Фигура 16. Честотните характеристики люлеенето члена.
единица честота отговор на логаритмичната амплитуда
При стойности 0.5 Фигура 17. Логаритмични честотни характеристики на люлеене в члена. Ако X<0,5. то получается заметный максимум (рис.17). Максимум характеризуется превышением Hm Опростената изчисляването да се намери Хм достатъчно приближение (виж фигура 17) .: Функцията преход на вибрационното ниво е показан на Фигура 18. Фигура 18. Функцията преход на вибрационното ниво. Когато X = 1 в един апериодични трептения изроди процес. Когато X = 0 колебания са ненамален (периодично), в който случай осцилаторна единица се нарича консервативно управление. Примери колебания връзки, показани на Фиг.19. Фигура 19. Примери колебания връзкидопълнителни материали