Иконометрия (9) - Инструкция, страница 3

14. Използване на прогнози регресионен модел. Точка и интервал прогнози

Прогноза се получава чрез заместване в регресия уравнението Y = a0 + a1x.

Тук a0, a1 - параметри, които се оценяват от статистически данни. Те се наричат ​​регресионни коефициенти.

В случай на Y при съвместното действие на няколко фактора (х1, х2. Xn) уравнението става

Y = a0 + a1x1 +. + Anxn.

В първия случай имаме чифт R. втората - в множествено число) променливи. Резултатът е оценка на средната стойност на зависимата променлива при тези нива на фактор от аргументи. За регресия уравнение обикновено се определя доверителни интервали, които могат да бъдат използвани за прогнозиране.

Прогноза точка - прогноза, която показва уникална стойност на прогнозираните фигурата. Конкретната стойност.

15. Нарушение на условия homoskedasticity: хетероскедастицитет, автокорелационната

Хетероскедастицитет и автокорелация на това нарушение на условия homoscedasticity (втори и трети условия Гаус-Марков). Обикновено се счита две възможности нарушение homoscedasticity условия:

1. грешки имат различни вариация за различните наблюдения - хетероскедастицитет. Хетероскедастицитет - "неравномерно разпределяне на" теоретично разпределение на случаен потребител е различен за различните наблюденията в извадката

Например, ако вземем предвид зависимостта от останалата част от разходите за заплати, е логично да се предположи, че разпространението ще бъдат по-високи за по-заможни хора.

2. Грешките имат постоянна дисперсия, но независим neyavlyayutsya Това явление се нарича автокорелация

В общия случай на една проста трансформация за постигане homoscedasticity По принцип:

1. Изчислете оценките на най-малките квадрати на регресионни коефициенти

2. Намерете остатъци ЗА и площади ei2

3. Намерете логаритмите на квадратите на остатъците LN (ei2)

4. Изчислява се регресия на LN (ei2)

5. предсказване LN (ei2) прог

6. Намери Wi тегла = EXP наблюдения (LN (ei2) прог)

7. получи Wi Тегловното се използва в претеглен метод на най-малките квадрати

Последици от хетероскедастичност и автокорелационни води до неефективност получената регресия коефициенти (но те остават безпристрастен) и до неправилно изчисление на наблюдаваната Т и F-статистика.

16. генерализирана малко метод на квадратите, Aitken теорема

Използването на обикновените най-малките квадрати, в нарушение на условията homoscedasticity води до следните негативните последици:

1. изчисленията неизвестни коефициенти β са неефективни, т.е. има и други оценки, които са безпристрастен и имат по-малка дисперсия.

2. стандартните грешки регресионни коефициенти са подценени, а оттам и т -Statistics - надут, и ще се получават грешна представа за точността на уравнението на регресия.

Генерализирана метод най-малките квадрати

Ние считаме, метода на оценка, когато homoscedasticity състояние, матрица е β = (Ω-1 XT X) -1 НТ Ω-1у

Изчисление на неизвестните регресионни коефициенти на това уравнение се нарича генерализирано най-малките квадрати (OLS).

Aitken теорема: в нарушение на оценките на предположения homoscedasticity получени генерализирана метод най-малките квадрати, са безпристрастен и най-ефективен (като най-малкият вариант). На практика, со матрицата почти никога не се знае. Така често се опитват всеки метод за оценка на матрица со за оценка и да ги използва за оценка. Този метод се нарича достъпни генерализирана метод на най-малките квадрати.

17. Тестове за хетероскедастичност: Spearman, Breusch-езически, бяло, Goldfeld-Quandt

Място корелация. тест за степен на съответствие на Spearman

Място за наблюдение на променлива - брой на променлива наблюдение в подреден възходящо последователност.

Тест Спиърман тест за степен на съответствие за хетероскедастицитет, се установи, че стандартното отклонение на остатъчния член на регресия има не-строга линейна връзка с обяснителна променлива.

Когато тестът корелация ранг на Spearman Предполага се, че случаен елемент дисперсия или ще се увеличи или намали с увеличаване на х и следователно в регресия, оценени от OLS, абсолютните стойности на остатъците и стойностите на х са несвързани помежду си. Данните за х и баланси са подредени. Ако приемем, че съответния общ коефициент корелация население е нула, т.е. Хетероскедастичност липсва, корелационен коефициент ранг има нормално разпределение със средна стойност 0 и дисперсия 1 / (п - 1) в големи проби.

Най-популярното официално критерий е критерий, предложен от Р. С. Квант и Goldfeld.

По време на изпитването съгласно този критерий се приема, че стандартното отклонение на разпределението на вероятностите ф пропорционална на стойността на х в това наблюдение.

Предполага се също така, че случаен термин обикновено се разпространяват и не подлежи на автокорелация.

С други думи Goldfelda- Квант тест - тест за хетероскедастицитет, който удостоверява, че стандартното отклонение на регресия остатъчен срок се увеличава, когато нарастващото обяснителна променлива.

Всички п забележки в пробата са сортирани по големина х, след което отделните регресия оценява за първи п 'и за последния N' наблюдения;

Средни (п 2n ') се изхвърля наблюдения.

Ако предположението за естеството на хетероскедастицитет е вярно, както и различията в последния N 'наблюдения ще бъде по-голяма, отколкото в първия N'. и това ще бъде отразено в сумата от квадратите на остатъците в двете "частни" регресии.

Ще означаваме сумата от квадратите на остатъците в регресии за първи N 'и последен N' наблюдения, съответно, чрез RSS1 и RSS2,

Ние се изчисли съотношението RSS2 / RSS1, който има разпределение с F (п '- к - 1) и (п' - к - 1) степени на свобода, където к е броят на обяснителни променливи в уравнението на регресия.

метод Goldfeld-Quandt може да се използва за тестване на хетероскедастичност предположи, че σ. е обратно пропорционална на х.

Използвайте същата процедура като тази, описана по-горе, но сега тест индекс статистика RSS1 на / RSS2, която отново има F-разпределение с (N 'к - 1) и (п' - к -1) степени на свобода.

Ще означаваме сумата от квадратите на остатъците в регресии за първи N 'и последен N' наблюдения, съответно, чрез RSS1 и RSS2,

Ние се изчисли съотношението RSS2 / RSS1, който има разпределение с F (п '- к - 1) и (п' - к - 1) степени на свобода, където к е броят на обяснителни променливи в уравнението на регресия

По този начин, тест Goldfeld-Квант се състои от три етапа:

всички наблюденията в извадката са сортирани във възходящ х.

взети първите и последните п наблюдения (една трета от всички), оценени две различни регресии и са RSS1 и RSS2

За връзка RSS2 / RSS1, провежда теста на Fisher (п '- к - 1) и горната част (п' - к - 1) по-ниски степени на свобода, където К - броят на обяснителни променливи в регресия.

Изпитването се прилага, при допускането, че дисперсията и зависи от редица допълнителни променливи:

1. Конструкция уравнението на регресия, и остатъците са изчислени:

2. Изчислява оценка на остатъците на промените:

3. Изграждане спомагателни регресия уравнение

4. За помощни регресионни уравнения определи обясни промяната на RSS.

5. Намерете статистическите данни от изпитването:

6. Ако хипотезата H0: homoscedasticity остатъци, че BP има статистики за разпределение. Т.е. присъствието на хетероскедастицитет на остатъците на нивото на значимост  предавания:

Когато хетероскедастичност може да се регулира:

Предполага се, че дисперсията, свързана с обяснителни променливи в следния вид:

защото дисперсии не са известни, те се заменят с площади оценява ei2 отклонения.

Алгоритъм приложение (например, три променливи)

1. Конструкция уравнението на регресия, и остатъците се изчисляват.

2. Оценка на спомагателната регресия уравнение:

3. Определяне на уравнението на спомагателни тест за значимост на

4. Проверете цялостното значение на уравнението с помощта 2 критерий.

Бял тест е по-общо от теста Goldfeld-Квант.

Недостатъкът на използването на тест Уайт: Ако отхвърляме нулевата хипотеза на homoscedasticity не е ясно какво да прави по-нататък.

18. Корекция на хетероскедастичност: логаритми, претеглена регресия, най-общия случай

Често наличието на хетероскедастицитет в регресия остатъците от посочва nepravelnoy модел спецификация.

Помислете два модела - линеен

Yi = SS0 + ß1xi + εi

Линейният модел на случаен prisudstvuet член в добавка форма, и по логаритмична модел - мултипликативна.

Мултипликативните форма отразява силното влияние на термина смущение за големи стойности на ковариати и по-слабите - за най-малките.

Ето защо, ако линейния модел има този вид хетероскедастицитет, това е напълно възможно, че в логаритмична модел не е хетероскедастичност.

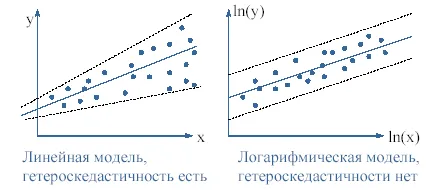
Логаритмична регресия не винаги е възможно да се отърве от хетероскедастицитет. В допълнение, логаритмична моделът не винаги отговарят на целите на изследването (задължително за оценка на зависимостта на абсолютната Velična вместо еластичност)

В тези случаи по-различен подход - претеглена регресия.

Yi = SS0 + ß1xi + εi

Нека Модел presudstvuet хетероскедастичност

И ние знаем точната стойност на дисперсията σi2 на модела грешка

(Следван от формули и решения, аз не мисля, че те трябва да се боя, така че аз няма да запушват светли умове с всички видове разтвори)

В края на краищата се изчислява. Така случаен член модел има постоянна дисперсия (изчислено е равен на 1) и следователно конвенционални OLS неизвестен koefitsent бъде безпристрастен и ефективен.

На практика, вариацията на грешката е почти никога. Но понякога може да се предположи, че σi2 е пропорционална на променлива зи а.

След това, теглата на наблюденията трябва да използват стойност 1 / ZI:

Вариацията на случаен потребител на такъв модел също е постоянна

Много често, като променлива, взаимосвързан с вариация на случаен член на регресор може да се използва:

В този случай, претеглената модел е както следва:

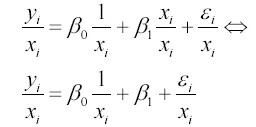
Koefitsent SS1 в трансформира модела съответства на свободен член.