ъгъл Math клас 10 между редовете в пространството

Ъгълът между две пресичащи се прави линии се измерва по същия начин, както в планиметрия (защото чрез тези линии могат да бъдат направени равнина). Така, ъгълът между две пресичащи се линии в пространството е най-малката от ъглите, образувани от лъчите на тези линии с връх в точката на пресичане.

Ъгълът между двете успоредни линии се приема за 0 или 180 °.

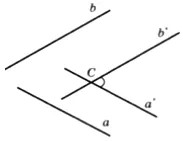
Ъгълът между две прави линии, пресичащи А и В е дефиниран както следва: през всяка точка С се извършва a'i греди б ", така че || а "и б || б ". Тогава ъгълът между А 'и В' се приема равен на ъгъла аб. С други думи, на линии А и Б са прехвърлени на нова позиция успоредна на себе си, преди да пресичат. По-специално, C точка може да се приема по една от линиите А и В, което в този случай е фиксиран.

Така, ъгълът между редовете се нарича кос ъгъл между пресичащи се линии, съответно, паралелни данни.

Перпендикулярни линии в пространството

Две линии се наричат ​​перпендикулярни в пространството, ако ъгълът между тях е 0 до 90

Лема: Ако една от двете линии перпендикулярни на трета линия, на другата линия, перпендикулярна на тази линия.

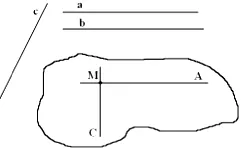
След т. М (М А, М и М в) извършва директно MA и МС || на || С. Тъй като с (с предположение), след това AMC = 90 °. От състоянието на || б и MA || а (според конструкцията) означава, б || MA (за теоремата на три успоредни линии). След това линиите В и С са успоредни съответно MA и MS, ъгълът между които 90 ° б ° С, както се изисква.

Тази линия се нарича перпендикулярна на равнината, ако тя е перпендикулярна на всяка права линия лежи на самолета.

(Може да записва: а α или α а).

Права линия, перпендикулярна на равнината пресича равнината.

и а с В, С, г.

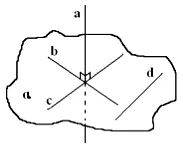
Ако едно от двете успоредни линии, перпендикулярни на равнината, и другата линия е перпендикулярна на тази равнина.

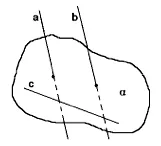
Равен в равнина алфа от произволен ред. Тъй като α, и след това с (по дефиниция). Чрез Лема, ако перпендикулярна с и Ь, както и успоредно с перпендикуляра. Тъй като в - произволна права линия и е перпендикулярна на алфа (по дефиниция). QED.

Ако 2 линии са перпендикулярни на равнината, тогава те са успоредни.

Ако линията не лежи в равнина, перпендикулярна на две пресичащи се линии в една равнина, а след това на правата линия и равнината, перпендикулярна.

m α, п α, т п = 0,1 м, 1 п

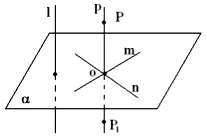
Начертайте линия р такава, че G р и р || 1. N 1 и р 1 || р п и р м. Нека P и Р1 - точка линия р, така че ОП = ОР1. След това, m и п - и по този начин оста на симетрия, α - средна равнина на симетрия на тези точки, а оттам и р алфа. и п р α || 1 α на януари. QED.

Свойствата на перпендикулярни линии и самолети:

1. Чрез всяка точка на пространство равнина се простира перпендикулярно на дадена линия.
2. Ако две равнини, а и б са перпендикулярни на линия, а след това те са успоредни.
3. Ако една от две успоредни равнини, перпендикулярни на права линия, а другата равнина е перпендикулярна на тази линия.

Теорема: Чрез всяка точка от пространството не принадлежи към равнината минава линия, перпендикулярна на тази равнина, а само един.

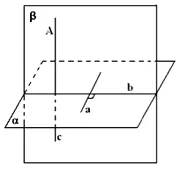
1. 1. Равен в алфа равнина и произволен ред; изгради равнина β α, преминава през т A β α = б β в равнината през направи линия с |. в α (в β и конструкция с, като β α). Така че, за да е желаната линия.
   2. Нека да докаже, че е само един. Да приемем, че това не е така и има пряка в1 алфа, а след това || С1. това не е възможно, тъй като С1 = А. По този начин, преминава през само една линия на равнината α.

QED.