Еквивалентност комплекти - studopediya

Определение 1.2. Ако всеки елемент от A е свързан с един уникален елемент от В и в същото време всеки елемент от B е свързан с един и само един от елементите на А. Твърди се, че между набори А и Б е налице 12:59 кореспонденция. комплекти А и В в този случай се казва, че е еквивалентен или equicardinal.

Комплектите еквивалентност са определени както следва:

Комплектът за еквивалентност е собственост на преходност.

Нека докажем този имот. От А

Б. след това за всеки елемент на Î И съществува уникален елемент б Î Б. Но тъй като B

С и след това за всеки елемент б Î В има уникален елемент в Î С асоциирано с този елемент член Î А. Това означава, че за всеки елемент на Î И там е уникален елемент в Î С, и за всеки елемент в Î С, има само един елемент на Î А. Следователно,

Очевидно е, че двете крайни множества са еквивалентни, ако и само ако броя на елементите в тях по равно. Например, набор А = и В = х. у. Z> еквивалент, А

Б. един към един кореспонденция може да се установи между елементи 4 и х. 5 и у. 6 и Z.

Множество ограничен мощност (обозначена çА ç) Е броя на елементите в този набор. Например, захранването е А = çА ç= 2.

Преди (Sec. 1.1), ние изследвахме множеството от всички подгрупи на набор А се нарича набор градуса и е означена Р (А). Множество Р (А) се състои от 2 п елементи. По този начин, çР (А) ç = 2 п.

Да разгледаме проблема за определяне на силата на комбиниране н ограничени серии.

Нека п = 2 и А и В - две пресичащи комплекти. Ние доказваме, използвайки Ойлер диаграма - Вен следната връзка:

çА ÈB ç= çА ç+ çB ç- çА ÇB ç, (1.1)

Фиг. 1.3 виждаме, че

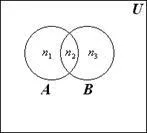
Формула (1,1) притежава също така и за случая, когато множество от А и В не се пресичат. В този случай,

çА ÈB ç= çА ç+ çB ç,

Да приемем, че п = 3 и А. В и С - три пресичащи комплекти. В този случай, следната зависимост притежава:

çА ÈB È C ç= çА ç+ çB ç+ çC ç- çА ÇB ç- çА ÇC ç- çB ÇC ç+ çА ÇB ÇC ç, (1.2)

Фиг. 1.4 виждаме, че

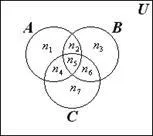
Това доказва с формула (1.2).

Формула (1,2) притежава също така и за случая, когато множество А. В и С са разместени. В този случай,

çА ÈB È C ç= çА ç+ çB ç+ çC ç,

Като цяло, на капацитета на свързване на набори от п се определя от формулата:

Тази формула е получена чрез индукция на п. [3].

Ако наборите Ai са разединени, т.е. Ai Çай = ÆАз ¹ й, ние получаваме частен случай на формула (1.3):

Като цяло, неравенството

Идеята на равностойност е подходящ и за безкрайните множества. Да предположим, например, A = N, ...>, В = п. ...>. Тогава A

Б. един към един кореспонденция е установена чрез правило елемент п Î А съответства на елемент - п Î Б. т.е. н «- п.

Б. един към един кореспонденция е установено съгласно правилото: п «2 п.

А = п ...> - набор от естествени числа, В = п. ... - 2, -1, 0, 1, 2, ..., п. ...> - множеството от всички числа.

Препишете от серията Б, както следва:

В = п. п. ...>, така че 0 е в първото място, втората -1, 1 на третия, четвъртия и -2 и т.н. Лесно е да се отбележи, че отрицателни числа ще застане на земята с четни числа, и 0 и положителни числа - в областта на нечетни номера. Следователно, едно към едно съответствие между серии А и В е избран в съответствие с правило: за всеки п ³ 0 елемент = 2n една от множеството А (т.е., нечетен елемент) съответства на елемент В = п от множеството В; а = 2n елемент от множеството А (т.е., дори елемент) съответства на елемент б = -п на множество В. По този начин, реализира едно съответствие между серии А и В. 1 "0, 2" 1, 3 "1 , 4 "-2 и т.н.

Примери 1.18 и 1.19 показват, че комплектът може да бъде еквивалентен на неговата подгрупа. По този начин, в Пример 1.18 B Ì А. и Пример 1.19 А Ì Б. И в действителност, и в двата случая A

Установяване на еквивалентността на комплекти, т.е. създаде едно към едно съответствие между техните елементи могат да бъдат различни начини. Фиг. 1-5 показва, че множеството от точки на два сегмента [а. Ь] и [С. д] еквивалент.

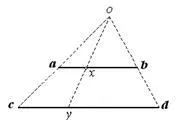
По същия начин комплекти може да се настрои за еквивалентност точки от два слота. На Фигура 1.6 е показано, че всеки набор от точки на интервала (а. В) е еквивалентен на множество точки за цялата линия.

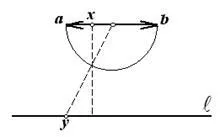
За да се гарантира еквивалентността на двете групи може да се използва следната теорема.

Bernstein теорема. Ако множество А е еквивалентна част от набор Б. серия В е еквивалентна на част от множеството набор A. А и В са еквивалентни.

Bernstein прилага теоремата, за да се докаже, че заданието на всеки сегмент е еквивалентно на множество точки на всеки интервал.

Нека А = [а. Ь] - произволен интервал, и В = (в г.) - произволен интервал.

По този начин, в условията на теоремата на Бърнстейн. Ето защо, A

Така че, всички интервали, сегменти и цялата линия еквивалент.