Един интегриран рисунка точка - studopediya
Теорема за проектиране на прав ъгъл.
Ако един от краката на прав ъгъл е успоредна на равнината на проекция, а вторият не заема стърчащ позиция (не е перпендикулярна на равнината на проекция), след това под прав ъгъл в равнината на проекция се очаква без изкривяване.
Горните цифри се наричат odnokartinnymi. Горните проекционни методи позволяват да се реши еднозначно прекия проблем - да се изгради проекция (рисунка) геометричен образ.
Проблемът с обратна на дескриптивна геометрия - за рисунка реконструкцията на геометричния образ - разрешен двусмислен (множествена или безброй решения). От това следва, че рисунката не е odnokartinny има свойството обратимост. Projection рисунка става обратима чрез добавяне на допълнителна информация.
В нашия Разбира се, ние ще се прилага обратима рисунка, който се нарича сложна рисунка в проекции (КС)
Chertezhomnazyvaetsya изготвянето комплекс, съставен от две или повече взаимносвързани ортогонална проекция изображения геометрична изображение.
Принципът на образование: геометрична изображението се проектира ортогонално поне две взаимно перпендикулярни равнини на издатъците, които след това подходящо комбинирани с една равнина.
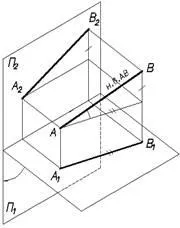
Point - nolmerny геометричен образ;
Символи на точки - А, В, С, D ... 1,2,3 ... и т.н..
Р2 (XOZ) - вертикален (отпред) проекционната равнина;
Фигура 6. Фигура 6 е чертеж на odnokartinnym.
Рисунката на фиг. 7, се нарича точка А комплекс рисунка.
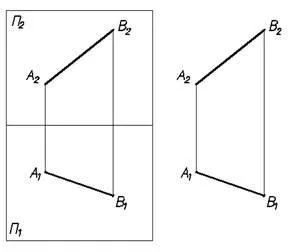
Както фигура (фиг.6 и фиг.7) е графична илюстрация на ортогонална проекция на същата точка А на две взаимно перпендикулярни равнини (Р1 и Р2).
Ако КС дадени две проекции на точка, можем да кажем, че точката е уникално определен на КС