Astronet - ао Упътване 1 турбулентност
- - интензитета на светлината в фокусната равнина като функция на ъгловото координира;
- - дължина на вълната на светлината;
- - диаметър отвор телескоп;
- - така наречената функция на Бесел.
Първият тъмен пръстен се намира в ъглово разстояние от центъра. Често това разстояние се смята за мярка за разрешаването на идеално телескоп.
Астрономически обект изображение може да се разглежда като множество от графични пиксели, всеки от които е описан от функцията Airy. Това може да се запише като намотка.
Ние наричаме това уравнение изображение. В сравнение с образа на обекта по-плавна и резолюцията намалява. Въпреки това, за определен диаметър на телескопа това влошаване - възможно най-малък. В този случай ние казваме, че резолюцията на изображението е ограничен от дифракция. ПРИМЕР астрономически изображения (галактическия център) с различни резолюции по-долу.
В: Как да им резолюция граници дифракция зависи от дължината на вълната?
Въпрос: изчисляване на дифракция-ограничена способност на човешкото око.
Какво се случва, ако телескопът не е идеална? Образът на точков източник не е толкова добър, колкото функцията Airy, резолюцията ще се влоши още повече. Но образът на уравнение ще остане в сила! По този начин, функцията точка спред (PSF) - това е всичко, което е необходимо да се характеризират образа. Ширината на PSF - е мярка за резолюцията.
Забележка: 1. Безусловно, ние се предположи, че в горните уравнения описва образа на звездата на единица интензивност, т.е. Тя е равна на неразделна над 1. Така, уравнение запазва пълен поток изображение от астрономически обект, само различни разпределя на пикселите.
Забележка 2. Приемаме, че PSF има същата форма в цялата зрителното поле. Това състояние се нарича isoplanatism. Това не винаги е вярно за астрономически изображения, особено при използване на АО, защото PSF се променя бавно през полето. В този случай, уравнението на изображения могат да бъдат приложени части на зрителното поле.
Форма PSF може да бъде неправилна; в този случай да се определи количествено резолюцията?
1. цялата ширина на половин максимум (FWHM) PSF.
2. Броят на съотношение Strehl, което означава, че централната интензивността на PSF в сравнение с централната интензивността на функцията Airy. Колкото по-висок коефициент на Strehl, толкова по-добре резолюцията. Дифракция-ограничено изображение - най-доброто, както винаги.
3. Енергия в кръга. По определение на интеграл от PSF е равно на 1. интеграл от PSF в радиуса на окръжност се нарича енергията в кръга. Тази характеристика е важно за наблюдения на слаби обекти, когато имате нужда от възможно най-добрите да се концентрира фотони.
Пример PSF с корекция турбулентност е показано по-долу.
Въпрос: Да предположим, че ФСФ стана два пъти вече, как да се промени съотношението Strehl?
Въпрос: Какво ще бъде отношението Strehl, идеално, ако половината от обектива на телескопа, за да се получи закъснение по фаза на?
Друг начин да се опише образа на уравнението - е използването на преобразуване на Фурие (FT, ще бъдат обозначени с тилда). Конволюция превръща в работа, и
Kolmogorov модел на нарушенията на турбулентност предписва специфичната форма на функцията фаза структура, а именно,
В тази формула само един параметър, който се нарича атмосферно последователност радиус, или пържени параметър. Като се има предвид, че дължината на пътя е безцветна, получаваме, че. Определяне винаги обърнат към съответната дължина на вълната!
Този модел, макар че може да изглежда примитивен, е в основата на цялата теория на изображения чрез турбулентност, включително адаптивните оптика. Разбира се, моделът не работи добре на големи (повече от няколко метра) и малка (по-малко от 1 см), разстояние, но се оказва, че това не е много важно.
Vorpos: Каква е средната квадратична разлика от атмосферното фаза дължината на база в радиани и дължини на вълните?
Въпрос: Ако видите при дължина на вълната 0,5 микрона, която все още е при дължина на вълната 2,2 микрона?
Сега ние поставяме този модел в атмосферните дълги експозиции ОТС, и да се получи под формата на:
Прилагането на трансформацията на Фурие на това уравнение, ние получаваме атмосферния PSF за дълги експозиции. Числени изчисления добив връзката между FWHM на атмосферния PSF (наречена или качество на изображението), и:
При дължина на вълната от 0.5 микрона, качеството на изображението 1 секунда съответства = 10.1 cm.
Strehl съотношение атмосферно PSF е точно същото, както за перфектно телескоп (това е причината за странен фактор 6,88) По този начин, за голям телескоп, съотношението на Strehl е проста.
Въпрос: Какво е съотношението Strehl за изображение с дълго излагане на 4-m телескоп на качество на картината 1 секунда на дължина на вълната от 0.5 и 2.2 микрона?
Пържени радиус понякога идентифицирани с характеристика мащаб атмосферни смущения. Това не е съвсем вярно: ние виждаме, че законът Колмогоров не разполага с характерен мащаб. Въпреки това, само смущение на размера на реда са важни за изображения с дълги експозиции. В по-малък мащаб изкривяване е много по-малък, отколкото в голям мащаб става толкова голям, че атмосферното ОСТ е нула.
Местната степента на турбулентните колебания на индекса на пречупване на въздуха е описан от индекс на пречупване структура константа, която се измерва в единици странно, т. Зависимост от профила на височина се нарича турбуленция. Качеството на изображението зависи от комбинирания ефект от всички слоеве на атмосферата:
където - височината, - ъгълът на зенит и интеграцията се осъществява от телескопа до максималната височина на турбулентността (около 20 км).
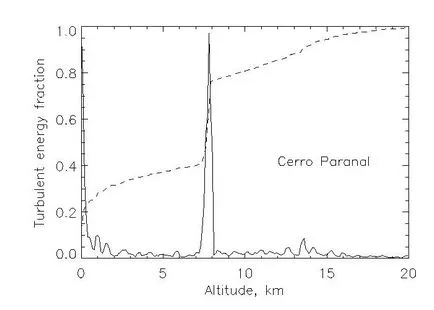
Тази фигура показва пример на профил на турбулентност в относителни единици в Серо Паранал (плътна линия). Съотношение на турбуленцията на определена височина се вижда от прекъснатата линия. Въпреки, че в този пример, значителна част от турбуленцията се концентрира в два слоя, все още около 1/3 от общата енергия е равномерно разпределена върху всички височини.
Въпрос: С помощта на тези отношения, да получите като качество на изображението зависи от ъгъла на наклона.
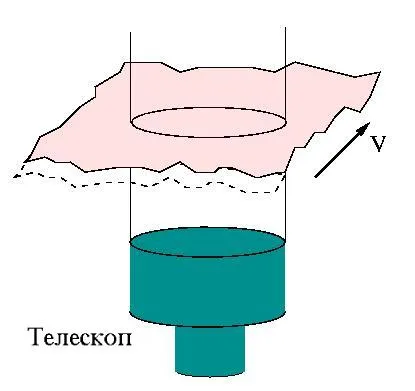
където - скорост на вятъра, среден ръст. Този параметър определя колко бързо трябва да бъде система за адаптивни оптика.
В. Като типична стойност = 20 м / сек, което е атмосферни времеконстанта при дължини на вълните от 0.5 и 2.2 микрона с изображение на една секунда?
Снимки на небесни обекти, заснети с експозиция или по-кратко се наричат изображения краткосрочни експозиция. Те съответстват на фиксираната (замразени) от атмосферни аберации. За по-дълги експозиции се осредняват аберации, и експозиции много по-дълго можете да получите PSF дълго излагане.
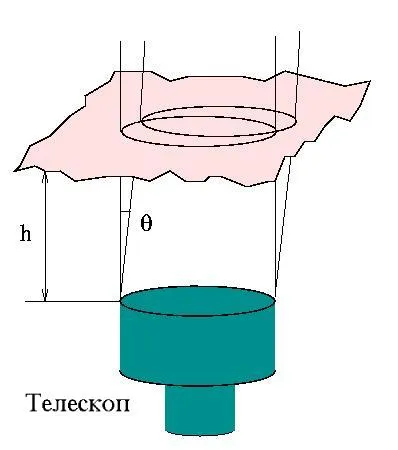
Стандартната определението на атмосферното isoplanatic ъгъл - тя
където - е характерна средна височина турбулентност. Вземете средно претеглена с профила, като резултат, за типични условия на достатъчно голяма височина км.
Въпрос: Какво е isoplanatic ъгъл за дължините на вълните на 0.5 и 2.2 микрона с изображение на 1 секунда?
Това явление е много голям проблем за адаптивни оптика, тъй като то ограничава разстоянието между контролния звезда и обект на изследване. Оказва се, че за повечето обекти не е подходящ (светли такива) референтни звезди, така че трябва изкуствени лазер водещите звезди. Като алтернативен метод, за да се увеличи коригира областта, можете да опитате да приложите триизмерен корекция на турбулентност (мулти-спрегнати адаптивни оптика. МСАО).
В оптика, отклоненията са често представени като сбор от специални полиноми, наречени Zernike полиноми. Случайни атмосферни отклонения могат да бъдат представени в същата форма; обаче, коефициентите на тези отклонения (отклонение, астигматизъм и т.н.) са произволни функции, които варират с времето.
Zernike полиноми са определени в полярни координати на обиколката на радиус единица. Те се характеризират с радиални и азимута за поръчка (за това, заема стойности между 0). Често, вместо двата индекса и последователното номериране с един индекс. За даден радиален цел съществуват Zernike полиноми.
Първите режими Zernike са наименувани същите като известни отклонения и имат прост смисъл (виж таблицата на първите 15 режимите Zernike).
Предимствата от използването на режима на Zernike произтичат от факта, че те са ортонормирана. т.е. скаларната продукта е равно на 1, ако и нула в останалите случаи. В скаларен продукт се определя като интеграл над отвора на телескопа:
Често ограничен брой видове Zernike вече дава достатъчно добро представителство на атмосферни аномалии. Ако тези режими са коригирани адаптивни оптика, тя създава изображение с качество, което е почти неразличима от определеното дифракция.
Мода бутало съответства на постоянна фаза, която не влияе на изображението. Обикновено, този режим се игнорира.
Въпрос 4-m телескоп разфокусира от 1 mm. Изчислява аберация срещащи се в продължение на 0,5 дължини на вълните и 2.2 микрона.
Въпрос: Да предположим, че атмосферното аберация съдържа само случайни склонове с равни амплитуди. Запишете съответната фаза структура функция.
режими Orthonormality Zernike предоставя лесен начин да се изчисли фаза дисперсия, интегрира по време на ученика. За един режим е то. Дисперсията на всички видове е сума от квадратите на коефициентите, започвайки от второто (буталата изключени).
В турбулентност модела на Kolmogorov, ние можем да получим статистическите свойства на коефициенти, съответстващи на аберации атмосферните фаза. Математически трансформации водят до проста формула:
Както можете да видите, Нол матрица е почти диагонал (но това не е така за по-висок ред). Защо не е фактор? За Колмогоров турбуленция е безкрайна! Въпреки това, на първия режим (бутало) е без значение към изображението.
Въпрос: 4 и качеството на изображението на телескоп 1 секунда, изчисли RMS амплитудата на наклона в радиани (с дължина на вълната от 0.5 микрона). Премести го средноквадратичната амплитуда на движение на изображението на звезда. Тя зависи от това дали амплитудата на вълната?
Какво се случва, ако се коригира първото модата, използвайки адаптивни оптика? Съответните коефициенти стават нула, и намаляването на общия фаза дисперсия. Означава средно над зеницата на фаза дисперсия като пишем
където първите режими Zernike са коригирани.
Пълен некоригиран атмосферно фаза отклонение (всички видове, с изключение на буталото) съвпадат. С други думи, телескоп с диаметър отвор атмосферно фаза вариация на е приблизително 1 кв радиани. Ако наклонът се коригира, а след това. Това означава, че се спуска до 87% от общия фаза дисперсия. Коригиране радиално около 2 до получаване на радиална порядъка на 3 оставя некоригиран дисперсия. Както можете да видите, по-нататъшното намаляване на корекция разрез фаза изисква увеличаване на броя на режимите Zernike.
За голям брой фиксирани режими (10 $ "ширина =" 61 "височина =" 34 ">, която се проявява в реални системи), един много полезен асимтотична формула за Нол:
Въпрос: С помощта на ценностите и на данните по-горе, се изчисли.
Колко режими трябва да бъдат поправени? Оптика знаят, че когато остатъчната фаза е по-малко от 1 радиан, качеството на изображението подходи дифракционната граница. Сега имаме всичко необходимо, за да се определи броя на режимите, като функция на диаметъра на телескопа, качеството на изображението и дължина на вълната! Достатъчно е да се запише и архивирате всичките формули (опитаме да го направим!). резултатът
Q: Колко Zernike видове трябва да се коригира на 4-т телескоп за изобразяване при дължини на вълните от 0.5 и 2.2 микрона с изображение на 1 секунда?
Необходимо е да се коригира с помощта на сътресенията режими Zernike? Разбира се, не фаза отклонения могат да бъдат измерени и коригирани използва всеки друг набор от базови функции или режими обикновено без да повлиява директно фронтът на вълната. Оказва се, че режима на Zernike - това е вторият набор от качествени събития (най-добрият набор от режими, наречена Karhunen-Loev). Изборът зависи от броя на наблюдаваните параметри (събития), необходими за постигане на желаната степен на корекция; за режима на Zernike е по-малко, отколкото за местен контрол на фронта на вълната.
Заключения. В тази глава основите на изображение в идеално телескоп и на наличието на отклонения (PSF, OTf, ограничи дифракция, съотношението на Strehl). След това на основните параметри на атмосферата, свързана с адаптивна оптика (функционални фазова структура, качеството на изображението, постоянното време и isoplanatic ъгъл). Проучихме разлагането на аберации на случаен фаза на режима на Zernike. Сега можем да се определи броя на събитията, които трябва да бъдат коригирани.