1 елемент база цифрова схема

Цифровият схема, два класа променливи се използват в съвременните цифрови устройства за обработка на информацията: цифрите и логически променливи.

Числата носят информация за количествените характеристики на системата, върху тях можете да направите аритметика, че аритметиката е базирана на цифрови устройства. А логически променливи определят състоянието на системата, или че тя принадлежи към класа на държави, които изграждат логическата рамка на цифрови устройства. Цифрите и логически променливи, свързани помежду си за решаване на задачи за управление и обработка на данни.

1.1 булева алгебра

При проектирането на логически схеми и цифрови устройства, като математически инструменти прилага алгебра на логиката или Булева алгебра е разработена в средата на деветнадесети век, ирландският математик Джордж Бул, по-нататъшното развитие и прилагане, получени през 1910 PS Ehrenfest през 1938 г. от Шанън.

Математическият основа за цифрови устройства е алгебра логика, която работи на променливи, като само две стойности, произволно определен 0 и 1, т.е. бинарни променливи. Функциите на бинарни променливи се наричат ​​логически. Те също така могат да се вземат само две стойности.

Логическата функция е функция на форма F (х1. X2. Xn). който, като му аргументи x1. x2. хп. може да се само две стойности - 0 или 1. За всяка логическа функция на п променливи съществува брой п = 2 п различни групи, и ако е определено тези набори от функция, такава функция се нарича напълно определени. По този начин броят на логически функции на п променливи (х1. X2. Xn) = 2 N = 2 2 п.

Ако функцията за логика не е определена за всички набори, това не е напълно сигурно, или underdetermined. На underdetermined функция определя стойността на променливите е обозначена с О и може да бъде произволно разширят определението или нула или едно.

Над променливите в логиката на алгебра могат да изпълняват три основни стъпки: логично добавяне (+, V) или операция ИЛИ (дизюнкция), логическата размножаването (ендо, ·.) Или работа и (заедно) и логично отрицание НЕ операция, или (инверсия):

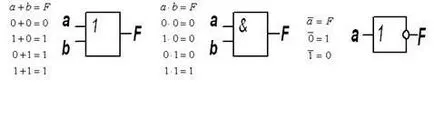
Логична функция може да бъде определена устно изразяване алгебрични или таблица, наречена маса кореспонденция или маса истина. Действия по бинарни променливи са произведени в съответствие с правилата на логически операции (законите на алгебра на логиката).

Основните закони на алгебра на логиката:

Логическите закони позволяват да се превърне първоначално логически функции и да ги доведе до форма, подходяща за по-нататъшна употреба.

1. комутативен право (закона на commutativity) за логическо размножаването и логическа добавяне: а · б = б · А; А + В = б + а.

2. асоциативен право (асоциативен право) за логическо размножаването и логическа добавяне: (а · б) · с = с · (б · в); (А + В) + с = а + (В + С).

3. закона на разпределение (разпределителни право): А + В · с = (А + В) (а + в);

4. право абсорбция: A + A · б = а · (1 + б) = а; на · (А + В) = а · A + A · б = а.

6. Правото на отрицание (законът на двойственост, закона на де Морган); ; - "Pierce стрелка" (функция "Webb"),

7. Законът на двойното отрицание :.

8. закона на умножение с 1 и 0. · 1 = а; на · 0 = 0; на · а = а.

10. Изключенията закона и противоречията :; ,

12. операция "XOR" (нееквивалентност, количеството на

13. Операцията сравнение (еквивалентността, еквивалентността):

Закони 1 - 10 показват, че логиката алгебра има двойственост имота (двойственост) по отношение на логически събиране и умножение операции. Двойствеността се дефинира като промяна на знаци върху операции и сделки знаци или знаци или всички операции или сделки подписва I.

Logic функция за удобство на запис и последващ синтез е изразено като сбор от продукти с променливи, или като продукти на техните суми. Първият запис се нарича разделителен нормална форма (DNF), а вторият - на съединителната нормална форма (CNF).

За всеки логически функции могат да съществуват няколко равностойни дизюнктивен и съединителната форми, но има само един вид CNF или DNF, в която функция може да се запише уникално (перфектни нормални форми и PDNF SKNF). В функция PDNF се изписва като единична логическа сума (mintermov) съставки, и в SKNF - логическа продукт съставки нула (makstermov).

един и нула съставки - комбинация от променливи, за които функцията съответно се отнася до един или нула.

Mintermom (. Или елементарен връзка Qi или съставна единица) е логично продукт на директни или обратни променливи, с всяка променлива в продукта се извършва само веднъж.

Makstermom (. Или елементарна дизюнкция Di или съставка на нула) е логическа сума на преките и обратни променливи, с случва всяка променлива в размер само веднъж.

Mintermov makstermov брой и предварително определен брой аргументи съответства на броя на различни набори от аргументи п = 2 п.

Имоти mintermov и makstermov:

1. Между Показатели I и едноименния mintermov makstermov н булеви променливи са следните отношения :. , където индексът I - десетично число съответства на двоичен код, съответстващ на комбинация от стойности на аргументи.

2. логично сумата от всички mintermov на редица фактори, равни на единство, т.е. ,

3. логичен продукт на всички makstermov на редица фактори, равна на нула, т.е. ,

4. Логически продукт mintermov с различни индекси е нула, т.е. Qi · Qj = 0. когато аз. к.

5. логично сумата от неравно makstermov равна на единство, т.е. Di + Dj = 1. когато аз. к.

За да се построи PDNF FCDHF функция логика на наш променливи, определени от масата за истина, е необходимо за всеки набор от променливи, в който функцията е на стойност 1, запис съвпад - тип minterm и всички такива съюзи за да се свържете признаци на разделяне. Променливите, които имат стойност нула, обърнати. , , Където - на десетични числа, съответстващи на набора от аргументи, на които F = Fi = 1.

За да се построи SKNF FCKHF функция логика на наш променливи, определени от масата за истина, е необходимо за всеки набор от променливи, в който функцията е настроена на 0, пише дизюнкцията - тип maksterm и всички такива дизюнкция свържете признаци на връзка. Променливите, които са обърнати важни единици :. където аз - на десетични числа, съответстващи на набора от аргументи, на които F = Fi = 0.

За да се намали броят на логически елементи, които реализират функция различни методи минимизиране. Чрез минимизиране на функцията за логика, за да намерите най-простите да се разбере представителство му под формата на суперпозиция, съставляващи всяка фиксирана функционално пълна система.

Логично функция може да бъде опростено чрез алгебрични трансформация директно използване на законите на булевата (свързване и усвояване). Но като правило, такива реализации изискват тежки изчисления, както и знания и умения. За функции, които имат по-голям брой променливи (повече от три), и по-голям брой думи, има специални техники. Най-често използваните методи, използващи Karnaugh карти и Veitch карти, представляващи правоъгълна маса с числото 2 п клетки. Всеки ред (колона) на тази маса съответства на определена комбинация от аргументи (променливи), всяка клетка отговаря на определен набор от стойности на аргументите, така че при всяко преминаване от една клетка към съседен по ред или колона променя стойността на само един аргумент на функцията. Karnaugh карти са различни от порядъка на аргументите Veitch помпа диаграма места, изброени в цикличен код (код на Грей) от двоични числа.

Алгоритъм за свеждане до минимум на функцията за логика се състои от следните етапи:

1. Логическата функция трябва да доведе до PDNF (SKNF). За да направите това, трябва да използвате законите на логиката алгебра 2, 3, 7-10, както и във всяка една от функциите на членовете, в които няма никакви аргументи, въведете израз на формата и да използва равенството за PDNF, където (за SKNF.) - отсъства в срок аргумент.

2. Напълнете mintermami (makstermami) правоъгълна маса, броят на които е равен на броя на възможно клетка mintermov 2 п. Mintermy логика функция маркирани 1 в съответните клетки на масата и makstermy - 0. Две minterma намира в съседните клетки могат да бъдат заменени от една единствена логическа продукт, съдържащ едно по-малко променлива, въз основа на разпределителни закони свързване и допълнение (размножаването) и 1 0. в общия случай, наличието на дялове (нули) 2 K съседни клетки елиминира К променливи.

3. При попълването на таблицата обкръжават правоъгълни контури на всички единици (нули). При извършване на вериги се придържат към следните правила: веригата трябва да бъде правоъгълна; в контура трябва да бъде само клетките, напълнени с 1 (0); броят на клетките във вътрешността на линия трябва да бъде цяло число от 2 мощност, т.е. 1, 2, 4, 8, 16; същата клетка изпълнен с 1 (0), може да бъде включена в повече бримки; най-долния и горния ред на таблицата, както и най-лявата и най-дясната колона се считат съседни; вериги трябва да са възможно най-малки, а самите контури - толкова голям, колкото е възможно.

4. Експресия минимум DNP функция (MDNF) се записва, както следва. Всяка верига е представена в член MDNF, където броят на променливите в К по-малко от общия п - брой на аргументи на функцията, т.е. равно на п - К. MDNF Всеки член е само на тези доводи за съответната верига са общи, т.е. са както инверсия или без инверсия. Като цяло, функцията може да има няколко минимални форми, които отговарят на различни, но равни по брой членове MDNF.

Например: Като се има предвид функция на четири променливи (аргументи)

Karnaugh карти, които правим, покривало

Напиши резултат под формата на покрити dezyunktsii съюзи (сбор от продукти):

Функцията за свеждане до минимум имаше 16 групи от променливи, след четири.